时间复杂度总结
| 问题 | 时间复杂度 | 备注 |
|---|---|---|
| 二分搜索 | $O(logn)$ | |
| 大整数的乘法 | $O(n^2)$或$O(n^{log_23})$….. | |
| Strassen矩阵乘法 | $O(n^3)$$O(n^{log_27})$$O(n^{2.376})$ | |
| 合并排序 | $O(nlogn)$ | |
| 快速排序 | 最坏$O(n^2)$最好$O(nlogn)$ | |
| 线性时间选择 | $O(n)$ | |
| 最接近点对问题 | $O(nlogn)$ | |
| 矩阵连乘 | $O(n^3)$ | 最优值在dp[0][n]处 |
| 最长公共子序列 | $O(mn)$ and $O(m+n)$ | 最优值在dp[m][n]处 |
| 最大子段和 | $O(mn^2)$或$O(m(n-m))$ | 最优值在dp[n]处 |
| 凸多边形最优三角剖分 | $O(n^3)$ | 最优值在dp[0][n]处 |
| 流水作业调度 | $O(nlogn)$ | 最优值在dp[m][n]处 |
| 0-1背包问题 | $O(min{nc,2^n})$ | 最优值在dp[i][j]处 |
| 活动安排问题 | $O(nlogn)$ | |
| 最优装载 | $O(nlogn)$ | |
| 哈夫曼编码 | $O(nlogn)$ | |
| 最小生成树 | P$O(n^2)$ K$O(eloge)$ | |
| 多机调度问题 | $O(nlogn)$ | |
| 装载问题 | 不记录$O(2^n)$,记录可以$O(2^n)和O(n2^n)$ | |
| 批处理作业调度 | $O(n!)$ | |
| 符号三角形问题 | $O(n2^n)$ | |
| n后问题 | $O(n!)$ | |
| 最大团问题 | $O(n2^n)$ | |
| 旅行售货员问题 | $O(n!)$ |
分支界限法不考虑复杂度,至少书上没写。
迭代法证明时间复杂度
$T(n)=aT(n/b)+f(n)$
设$n=b^k$则有
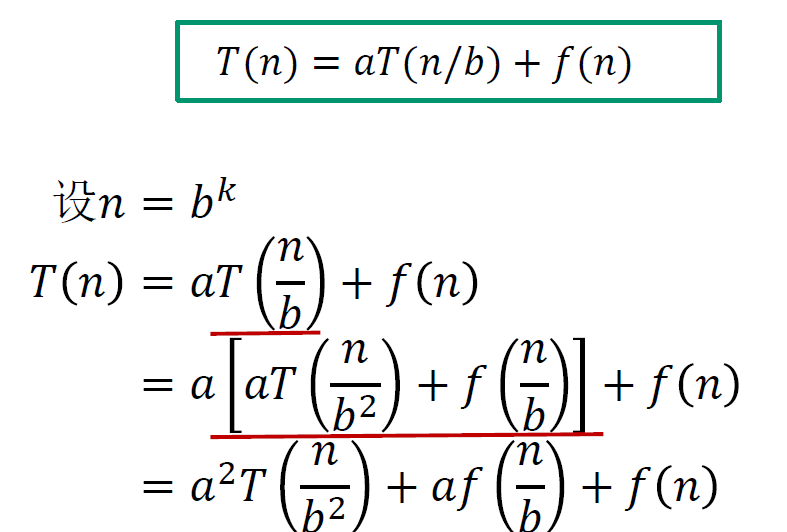

dp方程
矩阵连乘问题
$$\begin{equation} dp[i][j]= \begin{cases} 0& \text{i=j}\ min_{1<k\leq j}(dp[i][k]+dp[k+1][j]+p_{i-1}p_kp_j& {i\neq j} \end{cases} \end{equation}$$
公共子序列
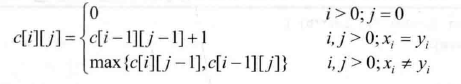
流水作业调度
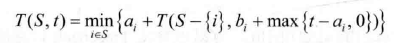
0-1背包问题
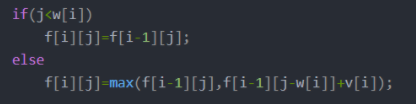
石子合并
两次矩阵连乘吧,背不会了
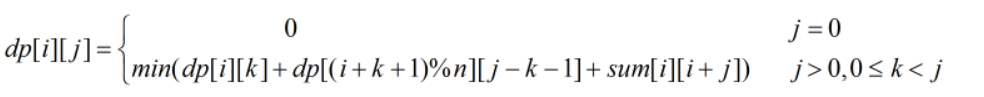
独立调度

最小子结构证明




贪心选择
最优装载

哈夫曼树

分支界限法的细节
首先队列的方案就不用多说了。就是一个队列+BFS。主要是优先队列的分支界限。
首先是0-1背包问题:
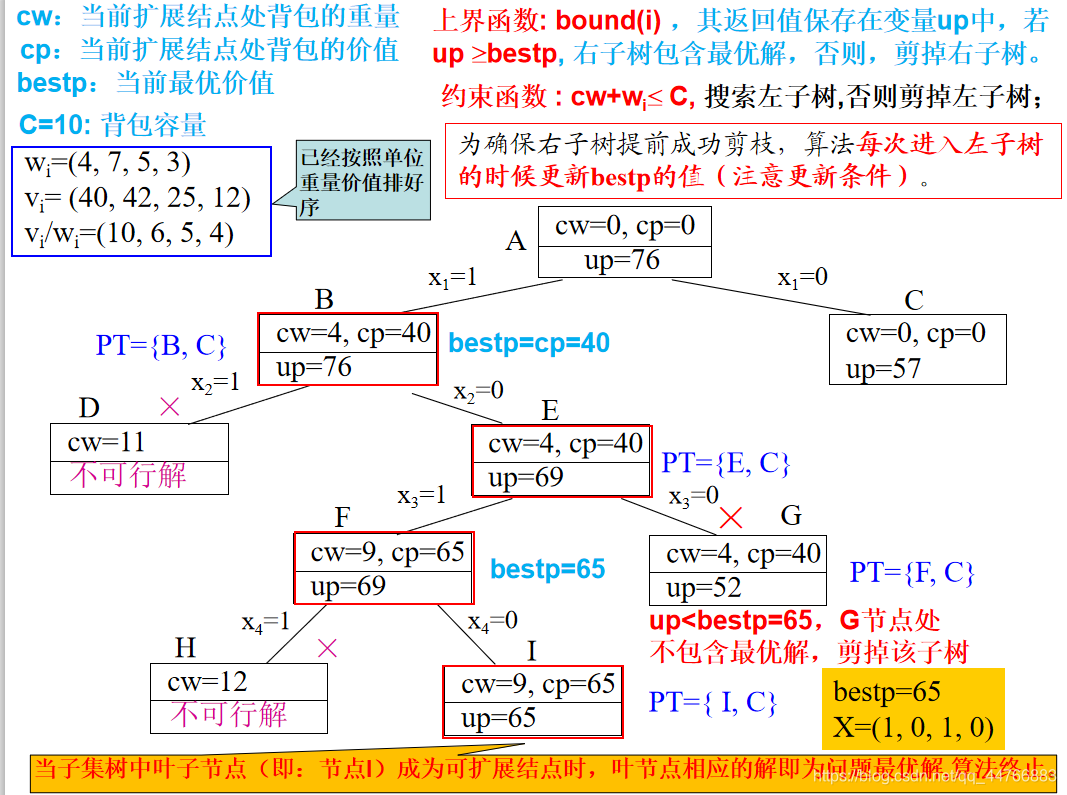
我们按照单位质量最高的排序,up表示当前可以实现的最优解。所以对于上述的树,首先是判断x1是否放入,如果放入,此时背包质量为4,价值为40,可能的最高价值为76。因为价值高于右子树,所以继续左子树遍历。接下来判断x2是否放入,显然,放不下,所以只能不妨,此时可能的最高价值为69,仍高于根节点的右子树。继续,判断x3是否放下,发现不仅可以放下,而且其可能的期望价值是高于不放的,所以右子树删掉,继续判断x4。发现放下去会超出背包重量,所以选择不妨,但是此时我们也能发现最优解的价值已经超过了右子树的价值,所以没必要继续遍历了。
接下来是装载问题。
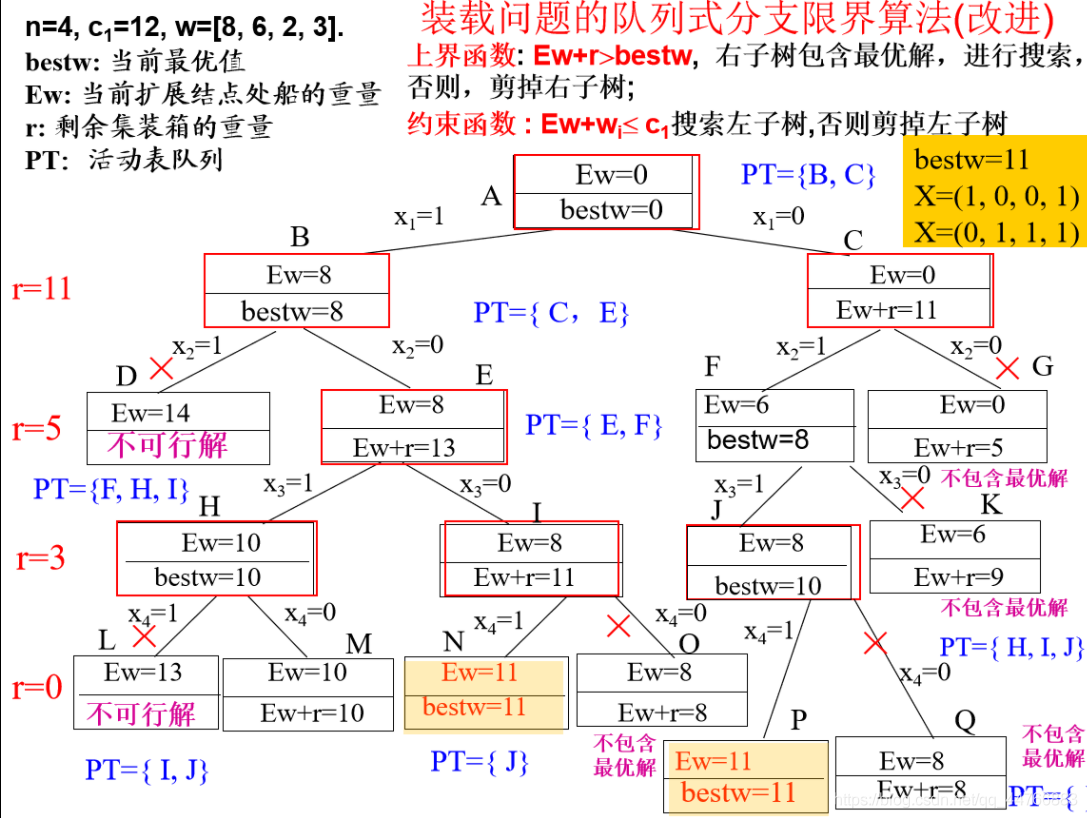
比较类似,只不过初始没有排序,而且这个例子比上面的复杂一点。x1还是放与不妨,但是放不放都挺好,所以先生成左子树,接着生成右子树。对于x2,第二个物品放不下去,所以不放,此时剩余物品的期望是13,但不是bestw,所以开始遍历根节点右子树的情况…
旅行商售货问题:
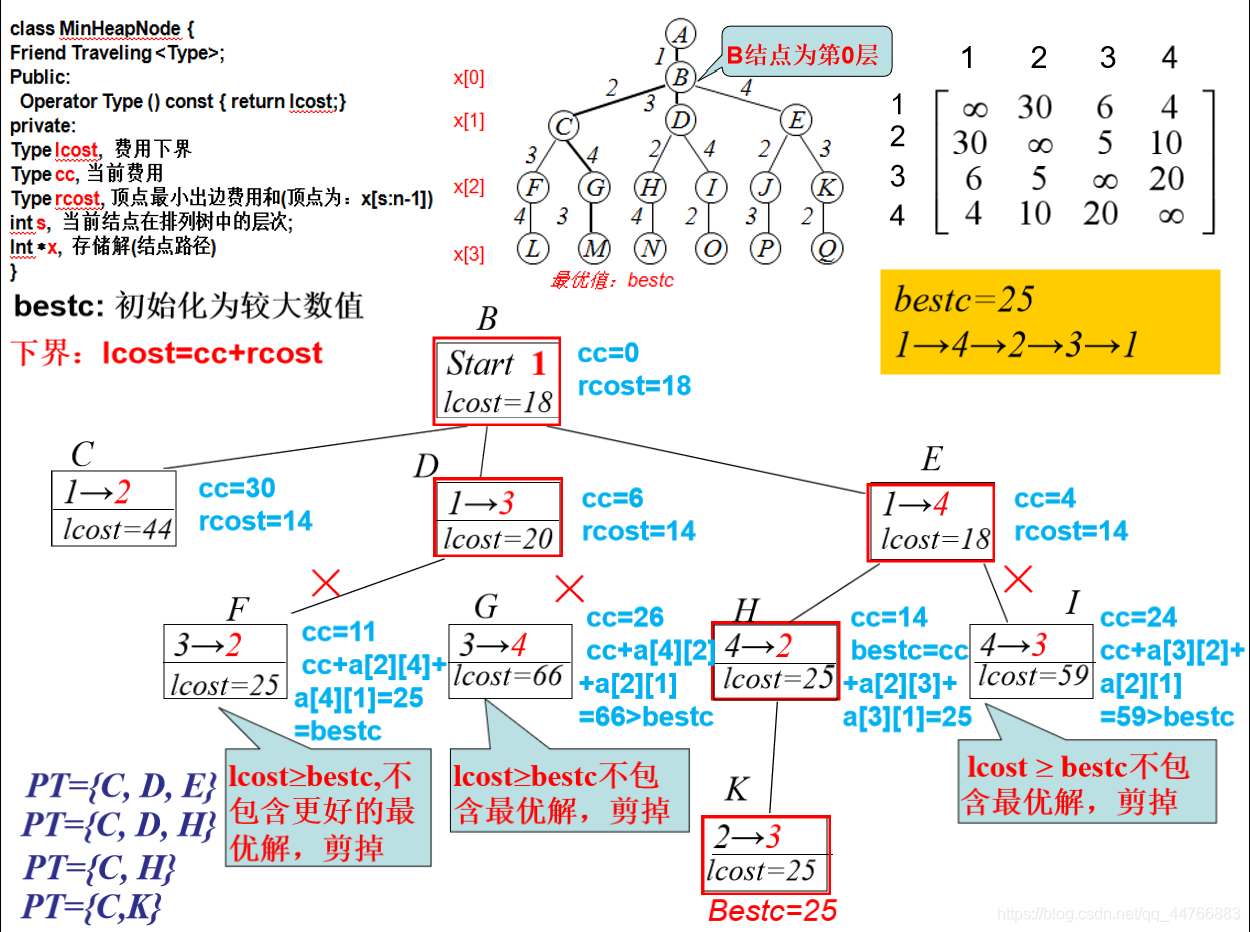
其他的
算法的要素:输入、输出、有限性、确定性
时间复杂度:
NP完全理论:
回溯法剪枝:是否超过约束条件、是否超出最优解。可能要画解空间
分支界限法:画队列变化情况
f