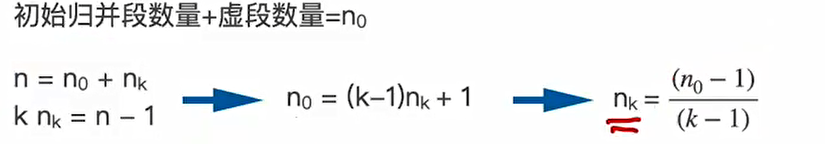数据结构
Some of watch
线性表
| 逻辑结构 | ||
|---|---|---|
| 顺序表 | ||
| 单链表 | ||
| 双(向)链表 | ||
| 循环链表 | ||
| 静态链表 |
栈、队列和数组
| 逻辑结构 | ||
|---|---|---|
| 顺序栈 | 栈空:S.top=-1;栈满:S.top=S.MaxSize-1 | 实际上会因为S.top的初始不同而不同 |
| 链栈 | 带不带头节点操作不同 | |
| 共享栈 | 0号栈空:top0=-1;1号栈空:top1=MaxSize;栈满:top1-top0=1 | |
| 顺序队列 | 队空:Q.front==Q.rear==0 | 进队和出队先操作元素后修改指针 |
| 循环队列 | 初始Q.front=Q.rear=1;队列长度:(Q.rear+MaxSize-Q.front)%MaxSize;队首+1:(Q.front+1)%MaxSize;队满需要分情况讨论:1、(Q.rear+1)%MaxSize==Q.front,2、Q.size==Q.MaxSize,3、tag==1 | |
| 链式队列 | 头指针指向头节点,尾指针指向尾节点。入队在尾指针、出队在头指针 | |
| 双端队列 | 只能拿来考试,输入受限和输出受限 | |
| 一维数组 | ||
| 对称矩阵 | 元素位置k=$\begin{cases} \frac{i(i-1)}{2}+j-1 & i\ge j\ \frac{j(j-1)}{2}+i-1 & i<j\end{cases}$ | 虽然有式子,但是建议自己推,因为下标可能会有不同 |
| 三角矩阵 | 同上 | |
| 稀疏矩阵 | 使用数组或是邻接表存储 |
栈的数学性质,n个不同元素入栈的出栈元素排列个数:$\frac{1}{n+1}\C_{2n}^n$
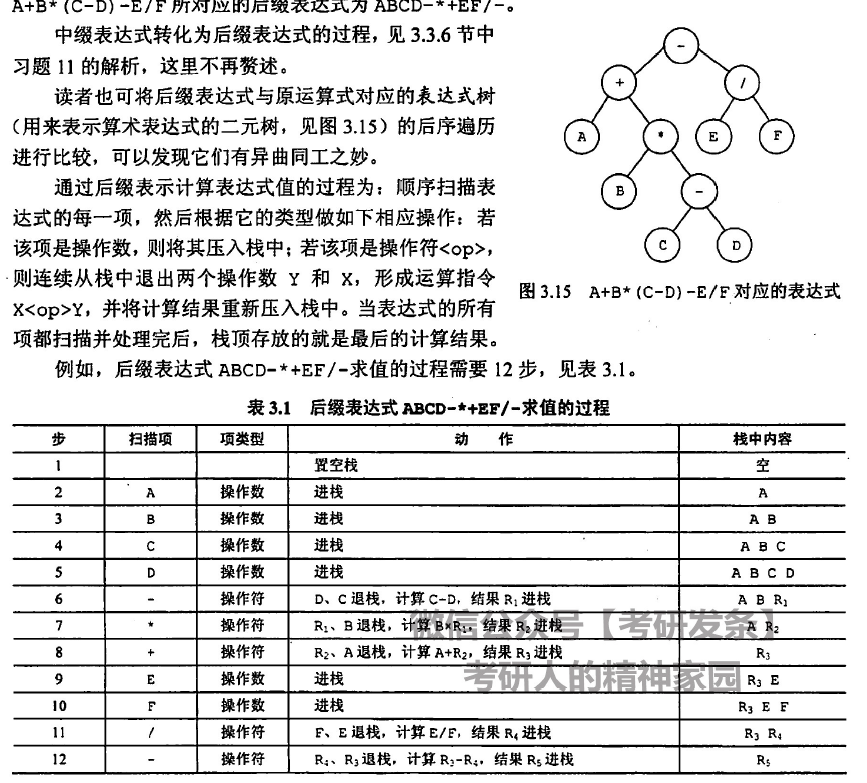
稍微注意下栈用于表达式求值:
串
乐,主要是KMP算法,也是唯一的算法
树
第一个大重点。
树的性质:
- 结点数=度数+1
- 度为m的树第i层最多有$m^{i-1}$个节点
- 高为h的m叉树最多有$(m^h-1)/(m-1)$(实际上就是等比数列前n项和)
主要考二叉树。满二叉树:拥有$2^n-1$个结点。完全二叉树:只有最后一层不满
二叉树的性质:
- $n=n_0+n_1+n_2=n_1+2n_2+1 \rightarrow n_0=n_2+1$
- 非空二叉树的第k蹭上至多有$2^{k-1}$结点
- 高度为h的二叉树最多有$2^h-1$
二叉树的遍历主要有先序、中序、后序、层序。其中只有先序中序 后序中序 层序中序
线索二叉树用于优化遍历,每个结点的结构由五个数据组成:lchild ltag data rtag rchild,当tag=0时表示指针指向孩子,当ltag=1表示左指针指向结点前驱,rtag=1表示右指针指向后继。通过增加线索,可以方便的进行遍历操作
二叉树完了之后是树、森林和二叉树之间的转换,在进行转换之前需要知道树的三种表示方式:双亲表示法使用线性表存储每个结点的父结点索引 孩子表示法每个结点的所有子节点用一个单链表存 孩子兄弟表示法每个节点有第一个孩子指针和右兄弟指针(实际上就是转二叉树

关于二叉树、树和森林的转换不必多说。另一个考点是关于数和森林的遍历,树的遍历有先根遍历 后根遍历森林的遍历分为先序遍历森林 中序遍历森林如果难记的话可以直接转为二叉树的遍历理解
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历(或叫后序遍历) | 中序遍历 |
数据结构包括:逻辑结构、存储结构和数据的运算。一个算法的设计取决于所选择的逻辑结构,而算法的实现依赖于所采用的存储结构。
树的应用:哈夫曼树 并查集
图
图是难度最大一章。
| 概念 | 定义 | |
|---|---|---|
| 简单图 | 不存在重复边、不存在顶点到自身边的图 |
|
| 多重图 | 与简单图相反 | |
| 完全图 | 对于无向图有$\frac{n(n-1)}{2}$条边,对于有向图有$n(n-1)$条边 |
|
| 子图 | 设$G=(V,E)$则$G’=(V’,E’)$其中$V’$是$V$的子集,$G’$是$G$的子集 | |
| 生成子图 | 在子图的基础上$V(G)=V(G’)$则为生成子图 | |
| 连通、连通分量、连通图 | 无向图中顶点之间有路径存在则称两个顶点是连通的 |
|
| 强连通图、强连通分量 | 有向图中两个顶点之间彼此都有路径则称两点强连通 |
|
| 生成树和生成森林 | ||
| 度、入度、初读 | ||
| 简单路径、简单回来 | 顶点不重复出现的路径 |
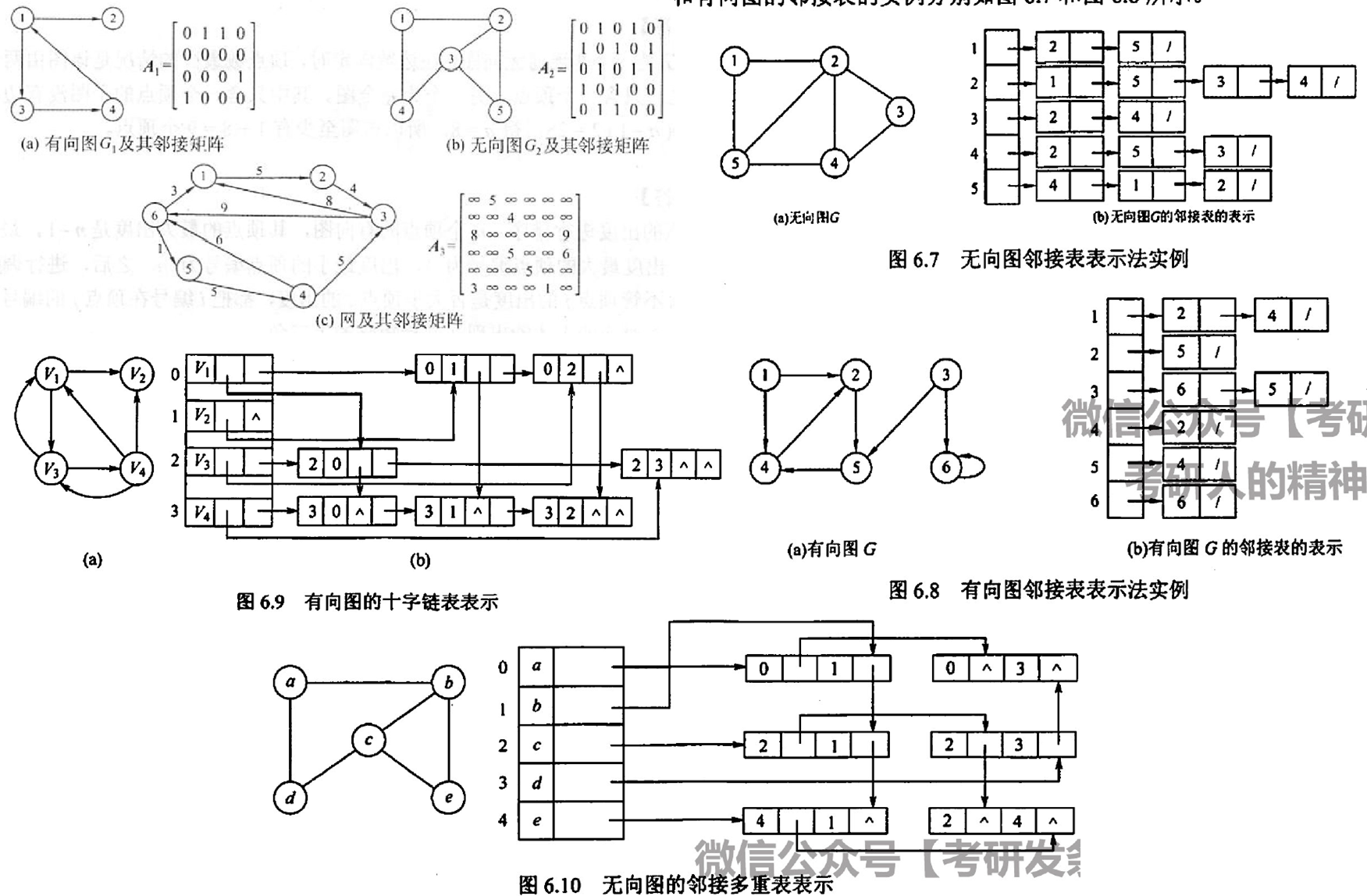
图的形态比较复杂,导致其存储方式也是相当复杂的:邻接矩阵 邻接表 十字链表 邻接多重表
| 遍历方法 | 复杂度 | |
|---|---|---|
| 广度优先遍历 | 时间复杂度取决于结构:邻接表 $O(V+E)$邻接矩阵$ O(V^2)$ |
用于解决单源最短路径问题、获取广度优先生成树 |
| 深度优先遍历 | 时间复杂度取决于结构:邻接表 $O(V+E)$邻接矩阵$ O(V^2)$ |
深度优先生成树 |
图的应用(应该是全数据结构量最大的地方了):最小生成树 最短路径 有向无环图描述表达式 拓扑排序 关键路径
| 应用 | 方法 | 思想 | 复杂度 |
|---|---|---|---|
| 最小生成树 | Prim | 从一顶点开始逐渐连接顶点(通常用于边稠密图) | $O(V^2)$ |
| Kruskal | 找权值最小边逐渐加入(适用于点多) | $O(ElogE)$ | |
| 最短路径 | Dijkstra | 求单源最短路径,做V-dist表格 | $O(V^2)$ |
| Floyd | 求各顶点最短路径,表格比较复杂 | $O(V^3)$ | |
| 有向无环图描述表达式 | —— | 根据二叉树来,并进行相同子式的共享 | |
| 拓扑排序 | 有手就行 | 可能有多种情况 | |
| 关键路径 | 麻烦的一批 | 无论从概念上还是计算上都是复杂且容易混淆的 | |
| ve | 事件最早发生时间,正向 | ||
| vl | 事件最迟发生时间,倒推 | ||
| e | 活动最早发生时间,正退 | ||
| l | 活动最迟发生时间,vl-活动时间 | ||
| d=l-e | 最迟开始时间 |
查找
除了时间复杂度,还要知道ASL(平均查找长度)
时间复杂度:
| 查找 | 时间复杂度 | 原理 | 备注 | ASL |
|---|---|---|---|---|
| 顺序查找 | $O(n)$ | 扫一遍 | 可以设置哨兵 | 成功$\frac{n+1}{2}$失败$n+1$ |
| 二分(折半)查找 | $O(logn)$ | 每次从中间开始,大往后,小往前 | $log(n+1)-1$ | |
| 分块(索引顺序)查找 | 自己算 | 块内无序,块间有序。块间二分,块内顺序 | 要求太苛刻了 | |
| 二叉排序树(BST) | $O(n)$ | 左节点小于根节点,右节点大于根节点 | 难在插入(不考虑插入相同元素)和删除(三种情况) | |
| 平衡二叉树(AVL) | $O(logn)$ | 左右高度差不能大于1,插入和删除时调整最小不平衡子树 | 相当蛋疼 | |
| 红黑树(RBT) | $O(logn)$ | 究极难 | ||
| B树 | 也不容易 | |||
| B+树 | ||||
| 散列查找 | $O(1)$ | 全场最佳 |
关键是蛋疼的树型查找:平衡二叉树、红黑树、B树,这里再强调一下红黑树(挺离谱的)和B树
尽管红黑树和二叉排序树的,平衡二叉树很容易被插入和删除破坏,所以要找平衡因子,而且需要重新计算。而红黑树不容易破坏红黑树特性,插入和删除时间开销很小(所以只查不插删就使用AVL,否则RBT)
红黑树首先是二叉排序树:

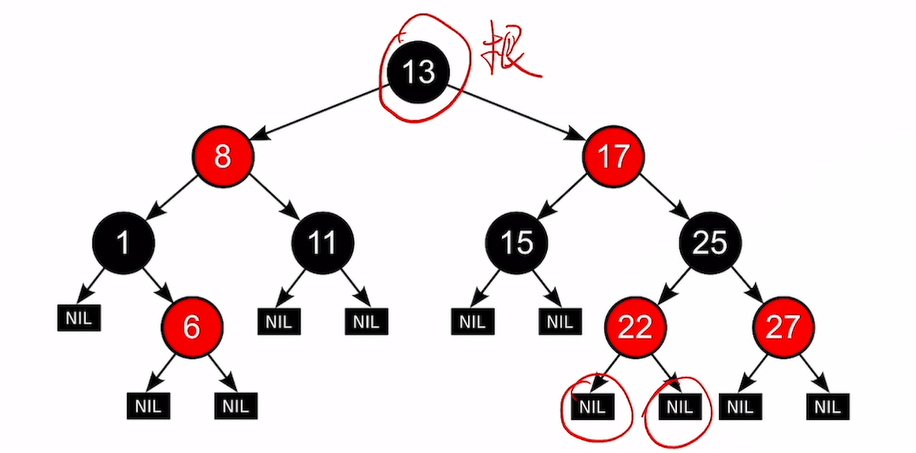
第5个性质就是堪比AVL的地方。黑高bh表示一个节点到达任意空叶节点的路径上的黑节点的数量。


插入只会破坏相邻不红的特性


B树n叉就有被n-1和关键字分为n个范围。为了使得查找和存储效率较高,一般我们通过认为m叉查找树中除根节点外至少有[m/2]个分叉,即m/2-1个关键字,且需要所有子树高度相同
叶子节点就是失败节点而终端结点指最后一层。

n个关键字必有n+1个叶子节点

B+树相较于B树,把区间换成了关键字。B+树支持顺序查找(子节点全部由链表连接),也可以通过树查找,非叶子节点都仅做索引,且为叶子节点中的最大值。
散列查找速度最佳,主要是处理冲突和散列函数(直接定址法、余数法、数则分析、平方取中)处理冲突有开放定址(线性探测法、平方探测法、双散列法)和拉链法
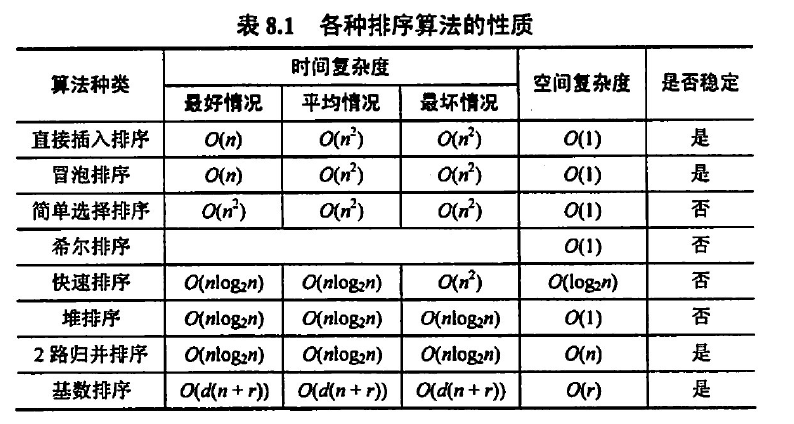
排序
| 排序 | 复杂度和稳定性 | 原理 | 备注 |
|---|---|---|---|
| 直接插入排序 | $O(n^2)$ 稳定 | 从前往后找元素,从后往前比,插入后后面的后移 | |
| 折半插入排序 | $O(n^2)$ 稳定 | 查找的时候使用二分查找 | |
| 希尔排序(缩小增量排序) | $O(n^{1.3})O(n^2)$ 不稳定 | 跨增量先排序,到最后一轮就相当于插入排序了 | 仅适用于顺序表 |
| 冒泡排序 | $O(n^2)$ 稳定 | 将最小的放前面或最大的放后面 | 每趟排序都会有一个回到自己的位置上 |
| 快速排序 | $O(n^2)$ 不稳定 | 分治法,每层找中间元素划分直到最底层 | 平均性能最优,每趟排序都会有一个回到自己的位置上 |
| 选择排序 | $O(n^2)$ 不稳定 | 找最小,次小元素逐渐往后排 | |
| 堆排序 | 建堆$O(n)$+排序$O(nlogn)$=$O(nlogn)$ 不稳定 | ||
| 归并排序 | $O(nlogn)$ 稳定 | 对相邻两组元素排序并合并,递归的进行 | |
| 基数排序 | $O(d(n+r))$ 稳定 | 根据数的特性进行,每次根据某个特性创造链并排序重整 |
主要有一个堆:顺序的完全二叉树,非叶子节点比左右孩子节点值大(大根堆)或小(小根堆)。处理非叶子节点从后往前,逐渐交换从而变为堆。排序的时候每次将堆顶和堆底交换,并重新调整堆。插入时放到最底然后调整,删除时将最后一个填充删除元素然后调整
外部排序关键在于考虑磁盘IO
归并排序中S趟归并总共需要的比较次数为$S(n-1)(k-1)=log_kr(k-1)=log_2r(k-1)/log_2k$ ,k为归并路数、n为元素
逻辑结构主要如下图:

存储结构分为:顺序存储、链式存储、索引存储(索引表)、散列存储(哈希)
算法具有5个特性:有穷性、确定性、可行性、输入和输出
算法的效率用时间复杂度和空间复杂度度量,其中时间复杂度一般考虑最坏的情况下的时间复杂度。原地工作指辅助空间为常量。
线性表:个数有限、逻辑上顺序、数据元素、类型相同、抽象
线性表的位序从1开始,数组下标从0开始
顺序表特点:随机访问、存储密度高
单链表存在一定的存储空间浪费,有无头指针在很大程度上会改变指针的各项操作(有头指针可以视空链表和正常链表为同仁)。
单链表、双向链表、循环链表、静态链表
栈是单口线性表:栈顶是允许插入删除的一端,栈底是固定的不允许插入删除的一端。
注意文字游戏:n个不同元素进栈的出栈个数有$\frac{1}{n+1}C_{2n}^n$
注意栈顶元素初始化值为-1还是0
共享栈:
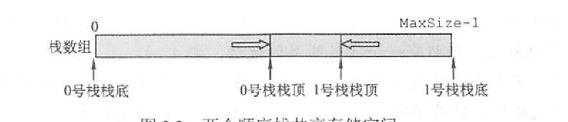
栈可以链式存储,但是头结点同样会对操作造成较大的区别
队列的队头出队列,队尾入队列。正常的队列会出现假溢出情况。
队头指针front必然是顺序表开始的位置,但是队尾不同,有可能是顺序表结束的位置,也有可能是下一个位置,操作同样不同。
循环队列的队头和队尾变化:
初始 front=rear=0
入队front=(front+1)%maxsize
出队rear=(rear+1)%maxsize
满的情况比较复杂,三种解决方案:牺牲一个位置区分,此时判满:(rear+1)%maxsize == front。令size=maxsize为满。增加tag,插入时满为tag=1,删除时空tag=0.
队列的链式存储,队头为链头。还有双端队列(两端均可以出入队列)
栈可以用于表达式求值,构建的输后续遍历即为后缀表达式,对应的也可以根据后缀表达式构建出原本的计算方式(从头往后,遇到操作符,出栈两个元素计算后入栈直至所有的元素被计算完成)。
栈还可以用于实现非递归(麻了),队列可以用于层序遍历(入队,出队时将元素的子节点入队)。
矩阵有较多表达形式,为了压缩矩阵的存储空间,这里设计了多种矩阵:
对称矩阵(存于一维数组)对应的$$k=\frac{i(i-1)}{2}+j-1$$下三角和主对角线;$k=\frac{j(j-1)}{2}+i-1$上三角区元素。上下三角矩阵类似。三对角矩阵则按行存取$k=2i+j-3$。稀疏矩阵可以使用索引记录(后面还有比较离谱的存储方式)
串给我爬
树应该是较难的一部分了,加上查找部分的红黑树,估计能和图两个人当老流氓了。不过DS好就好在理解就能解决绝大多数问题。
几个基础概念,树的高度、深度、度、层次、路径、森林
树的几个等式:树的结点数=度数和+1
二叉树是考察最多的内容,满二叉树和完全二叉树(注意两者不一样)、二叉排序树(左孩子小根,右孩子大根)、平衡二叉树
二叉树的几个等式:$n_0=n_2+1$完全二叉树的高度、结点数判定和计算
二叉树的存储分为顺序存储和链式存储,前者层次遍历,空节点设为0,后者是通常采用的方式,这里主要学习链式二叉树
链式的二叉树的先序中序后序遍历和如何转化为非递归算法(都是用栈),层次遍历用队列。遍历节点确定二叉树:知道先序和后序无法唯一确定,知道中序和层序可以确定
线索二叉树在二叉树的基础上加了ltag和rtag分别表示左右节点是前驱还是后继(0表示孩子、1表示后继),注意的一点是只有空结点需要用上tag标志,线索二叉树的线索如何指则取决于遍历方式。
树和森林的重点在于存储结构和转换(二叉树的存储结构不一定能用来存树)。树的存储通常有:双亲表示法(用顺序表存储)、孩子表示法、孩子兄弟表示法(这种方法常用于转二叉树)。
树与森林与二叉树的转换就没什么好说的了。
遍历方式:(通用方法就是将树和森林转为二叉树后遍历)
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历(后根遍历) | 中序遍历 |
哈夫曼和并查集(建议理解一手原理)
图是第二个流氓,有向图,无向图,简单图、多重图(不讨论)、完全图、子图(又有所有节点即可)、连通、连通图、连通分量(注意,连通分量指子图不是量),强连通(对应于有向图),生成树、生成森林(极小连通子图只有单边连接)、顶点的度、入度、出度
图的存储方式也有一车:邻接矩阵法(A[i][j]来表示i和j节点之间的边),邻接表法(解决邻接矩阵的稀疏问题,使用链表),十字链表(存有向图的,弧节点有5个域而顶点节点有3个域,关于这部分的细节建议好好看书)
图的遍历有深度优先和广度优先
图的应用更是重量级:最小生成树(kruskal、prim),最短路径(dijkstra、floyd),拓扑排序,关键路径(每个都能一道大题)
生成树:Prim取点集合,找距离最小的点。Kruskal,找能使连通的最小边
最短路径:Dijkstra(动态的贪心)从源点开始,每次选择最小的路径更新其它点,O($V^2$),不适用于负权值。Floyd求出全部的之间的最短,$O(V^3)$允许负权值,主对角线扫描
拓扑排序:依次删除入度为0的点
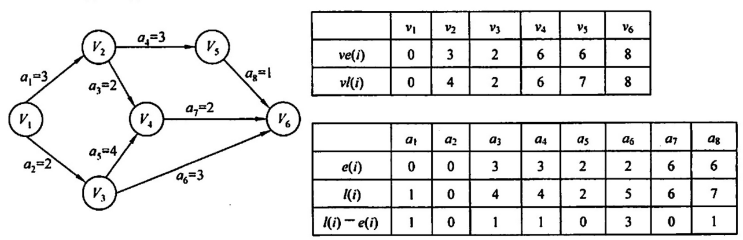
关键路径:事件最早的发生时间ve,事件最迟发生时间vl,活动最早开始事件e,活动最迟开始时间l,d=l-e。

关键路径不唯一,e正求,l反求,d=0即为关键路径
查找有新增了个重量级——红黑树
时间复杂度:
| 查找 | 时间复杂度 | 原理 | 备注 |
|---|---|---|---|
| 顺序查找 | $O(n)$ | 扫一遍 | 可以设置哨兵 |
| 二分(折半)查找 | $O(logn)$ | 每次从中间开始,大往后,小往前 | |
| 分块(索引顺序)查找 | 自己算 | 块内无序,块间有序。块间二分,块内顺序 | 要求太苛刻了 |
| 二叉排序树(BST) | $O(n)$ | 左节点小于根节点,右节点大于根节点 | 难在插入(不考虑插入相同元素)和删除(三种情况) |
| 平衡二叉树(AVL) | $O(logn)$ | 左右高度差不能大于1,插入和删除时调整最小不平衡子树 | 相当蛋疼 |
| 红黑树(RBT) | $O(logn)$ | 究极难 | |
| B树 | 也不容易 | ||
| B+树 | |||
| 散列查找 | $O(1)$ | 全场最佳 | |
平衡二叉树单拉出来,调整时有四种方式:LL(右单),RR(左单),LR(先左后右),RL(先右后左),L和R分别表示插入的顺序,LL就是左子树的左子树,类推。
装填因子的概念
常见的排序就没什么好说的了,关键是一些新的排序方式
| 排序 | 复杂度和稳定性 | 原理 | 备注 |
|---|---|---|---|
| 直接插入排序 | $O(n^2)$ 稳定 | 从前往后找元素,从后往前比,插入后后面的后移 | |
| 折半插入排序 | $O(n^2)$ 稳定 | 查找的时候使用二分查找 | |
| 希尔排序(缩小增量排序) | $O(n^{1.3})O(n^2)$ 不稳定 | 跨增量先排序,到最后一轮就相当于插入排序了 | 仅适用于顺序表 |
| 冒泡排序 | $O(n^2)$ 稳定 | 将最小的放前面或最大的放后面 | 每趟排序都会有一个回到自己的位置上 |
| 快速排序 | $O(n^2)$ 不稳定 | 分治法,每层找中间元素划分直到最底层 | 平均性能最优,每趟排序都会有一个回到自己的位置上 |
| 选择排序 | $O(n^2)$ 不稳定 | 找最小,次小元素逐渐往后排 | |
| 堆排序 | 建堆$O(n)$+排序$O(nlogn)$=$O(nlogn)$ 不稳定 | ||
| 归并排序 | $O(nlogn)$ 稳定 | 对相邻两组元素排序并合并,递归的进行 | |
| 基数排序 | $O(d(n+r))$ 稳定 | 根据数的特性进行,每次根据某个特性创造链并排序重整 |
堆:顺序的完全二叉树,非叶子节点比左右孩子节点值大(大根堆)或小(小根堆)。处理非叶子节点从后往前,逐渐交换从而变为堆。排序的时候每次将堆顶和堆底交换,并重新调整堆。插入时放到最底然后调整,删除时将最后一个填充删除元素然后调整
外部排序:指数据量太大内存放不下需要外存和内存多次交换。由于磁盘IO时间多于排序时间,因此时间主要考虑访问磁盘的次数。
通常使用归并排序,增大归并路数或者减少初始归并的段数能够提高速度

增加归并的段数会导致关键字比较次数的增加,所以可以考虑使用败者树:

其中叶子节点实际并不存在而非叶子节点存储着索引
置换选择排序用于减少段数。若工作区中的所有元素均小于构件的归并段中的最大值,那么停止归并段的构造。
由于置换选择排序减少了归并段的数量,当使用归并树对归并段进行排序时,读写的数量取决于归并段的块数,在这种情况下,建议使用哈夫曼树进行处理。但是在多路归并的时候会遇到最后一层结点数不够的情况,这时候需要设置长度为0的虚段,从而减少读写次数。需要补充的虚段的数量就是k叉树缺的结点数