Attention Please
首先,Attention算是Transformer中的一个小的结构,但是由于其重要性和有效性,在现在的各种模型结构都变得越来越常见,因而需要多次反复详细理解。虽然整体来说不复杂,但是由于至今的变体过多且细节实际上比较细,因此还是需要很多关注的。后续可能从以下几个部分依次说明。
- 手搓一下: Self-Attention - MHA - GQA - MQA - MLA
- 位置编码: RoPE
- 并行加速: FlashAttention
当然,除此之外还会有相当多的小tips用来补充。接下来就依次进行吧,
SDPA - MHA - GQA - MLA
Attention Is All You Need
Attention(注意力)机制如果浅层的理解,跟他的名字非常匹配。他的核心逻辑就是「从关注全部到关注重点」。对于Attention的机制已经有诸多的详细说明和讲解了。这里先简要说一下。
Attention的原始论文出自Attention Is All You Need。在该论文中提出了SDPA(Scaled Dot-Product Attention)和MHA(Multi-Head Attention)。
Self Attention 并不是特定的一个Attention结构,与Self Attention对应的是 Cross Attention。Self Attention指的是Q K V均来自一个数据的Attention计算,而Cross Attention则特指Q和 (K V)来自不同数据的Attention。
注意:之后的Attention都是基于Torch实现的。关于模型结构的实现,可以通过nn.Module实现一个__init__和forward,也可以类似现有的实现只完成函数即可。在此根据情况会说明并尽量贴出官方的代码。
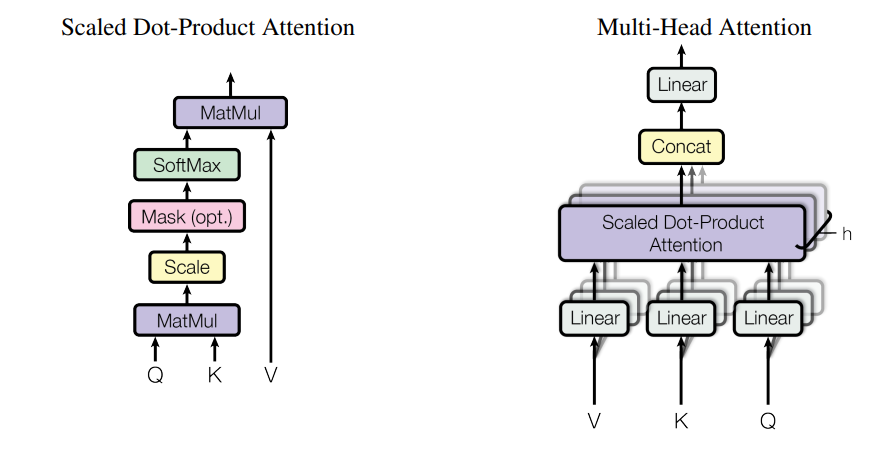
对于SDPA,整体的架构就是一个QKV的乘法,然而对于MHA,则稍微有点复杂,这一点我们后面再说,我们先详解一下SDPA。
首先,最原始的Attention公式是这样的:
$$Attention(Q, K, V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
因此SDPA的代码如下:
# https://pytorch.org/docs/stable/generated/torch.nn.functional.scaled_dot_product_attention.html
def scaled_dot_product_attention(query, key, value, attn_mask=None, dropout_p=0.0,
is_causal=False, scale=None, enable_gqa=False) -> torch.Tensor:
""" query, key, value : 与W_q, W_k, W_v相乘后的结果
attn_mask : 在Causal时做mask的mask
scale: 分母的放缩
enable_gqa: GQA 虽然很简单,但是后续再说
"""
L, S = query.size(-2), key.size(-2)
scale_factor = 1 / math.sqrt(query.size(-1)) if scale is None else scale
attn_bias = torch.zeros(L, S, dtype=query.dtype, device=query.device)
if is_causal:
assert attn_mask is None
temp_mask = torch.ones(L, S, dtype=torch.bool).tril(diagonal=0)
attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
attn_bias.to(query.dtype)
if attn_mask is not None:
if attn_mask.dtype == torch.bool:
attn_bias.masked_fill_(attn_mask.logical_not(), float("-inf"))
else:
attn_bias = attn_mask + attn_bias
if enable_gqa:
key = key.repeat_interleave(query.size(-3)//key.size(-3), -3)
value = value.repeat_interleave(query.size(-3)//value.size(-3), -3)
attn_weight = query @ key.transpose(-2, -1) * scale_factor
attn_weight += attn_bias
attn_weight = torch.softmax(attn_weight, dim=-1)
attn_weight = torch.dropout(attn_weight, dropout_p, train=True)
return attn_weight @ value
size of attention
上述代码我们分块来进行,首先是size的问题,虽然可以忽略但是还是详细说明一下吧。
L, S = query.size(-2), key.size(-2)
attn_bias = torch.zeros(L, S, dtype=query.dtype, device=query.device)
这里分别获取了两个数值L和S,对于QKV,其中KV的维度是相同的,均为$(N,…,H,S,E)$但是Q的维度为$(N,…,H,L,E)$,其含义如下:
- $N$: Batch size
- $H$: Head num
- $S$: 源seq_len
- $L$: 目标seq_len
- $E$: embedding dimension
初看这里有一个很奇怪的地方,为什么S和L是两个东西,实际上当S==L,即Query和KV输入相同时,此时对应的是self-attention,相对的,如果S!=L,则对应的是cross-attention。这里我们假设两者相同,即self attention情况。
对于输入维度为$(N, S, E)$,首先与Q,K, V参数矩阵进行矩阵乘法,其中QKV的参数矩阵均为$(E, E)$则在进行矩阵乘法时能够保证最后的E维度不变。
实际上这里稍微省略了一点,由于在Attention计算中是先进行QK乘法的,为了保证输入输出维度相同,实际上只需要保持V参数矩阵的输出维度为$E$即可。假设QK矩阵维度为$(E, X)$,则完成矩阵乘法后维度为:$(N, S, X)$,将两者进行矩阵乘法,得到的输出为$(N, S, S)$。同理,对于V参数矩阵,我们令其为$(E, Y)$,则完成矩阵乘法后的维度为$(N, S, Y)$。在SDPA中,直接进行$(N,S,S)和$(N,S,Y)$乘法即可,而且是可行的,因此输出为$(N,S,Y)$
注意,上述分析同时引出了一个细节:
- 哪些参数可以修改:由于Attention要求输入输出维度相同,因此,最后的Y实际上是等于E的。因此V矩阵的输出和hidden_size有关。其次,X实际上在计算的时候会消除,因此X数值是可以任意设置的。
完成上面的分析之后就可以轻易地知道上面两行代码是什么含义了。
scale it
scale_factor = 1 / math.sqrt(query.size(-1)) if scale is None else scale
这个倒是很好理解,因为完成QK之后需要进行softmax操作,因此进行scale有两个优势:
- 这取决于softmax函数的特性,如果softmax内计算的数数量级太大,会输出近似one-hot编码的形式,导致梯度消失的问题,所以需要scale
- 那么至于为什么需要用维度开根号,假设向量q,k满足各分量独立同分布,均值为0,方差为1,那么qk点积均值为0,方差为dk,从统计学计算,若果让qk点积的方差控制在1,需要将其除以dk的平方根,使得softmax更加平滑
casual it
if is_causal:
assert attn_mask is None
temp_mask = torch.ones(L, S, dtype=torch.bool).tril(diagonal=0)
attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
attn_bias.to(query.dtype)
if attn_mask is not None:
if attn_mask.dtype == torch.bool:
attn_bias.masked_fill_(attn_mask.logical_not(), float("-inf"))
else:
attn_bias = attn_mask + attn_bias
由于大模型采用的是因果注意力机制,对于中间$Q@K^T$的矩阵(前面提到了,输出维度为$(N,S,S)$),将其进行Mask操作,将上三角部分设置为$-inf$值,从而使得每个token只关注之前的数值而不具备对整个文本的理解。这里同样有几个细节知识点。
-
为什么使用causal注意力机制(或者说为什么大模型都使用纯decoder架构):提高训练难度;苏神提到了这个过程是秩满的因此效果更好
-
为什么填充的值为-inf:因为softmax是这样的。
从上面的代码逻辑可以看出来,在因果注意力机制条件下,需要对上三角进行一个填充:
>>> L = S = 4
>>> torch.ones(L, S, dtype=torch.bool).tril(diagonal=0).logical_not()
tensor([[False, True, True, True],
[False, False, True, True],
[False, False, False, True],
[False, False, False, False]])
实际上上述的代码逻辑有点问题,causal和mask必须一同给出。因此在完成attn_bias的获取之后,需要再在attn_mask上进行一下位操作,最后加到一起,注意,这里的attn_mask和causal mask不是一个东西,后者是decoder架构导致的,而前者则是可以在数据集中提供用于屏蔽token的额外操作。
SDPA operation
attn_weight = query @ key.transpose(-2, -1) * scale_factor
attn_weight += attn_bias
attn_weight = torch.softmax(attn_weight, dim=-1)
attn_weight = torch.dropout(attn_weight, dropout_p, train=True)
return attn_weight @ value
接下来再看就容易多了,前面都讲差不多了,key.transpose(-2, -1)就是转置,中间加上attn_bias掩码,在记性softmax操作,最后和value相乘。这就是SDPA的完整流程了。值得注意的一点是softmax操作是在dim=-1维度进行的,即每一行的所有token进行的,因此结果如下,实际上是一个下三角矩阵。
tensor([[1.0000, 0.0000, 0.0000, 0.0000],
[0.5000, 0.5000, 0.0000, 0.0000],
[0.3333, 0.3333, 0.3333, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500]])
至于dropout操作,现在的一些模型设置通常是把dropout概率设置为0的,不过这一点见仁见智吧。
至此,对于SDPA的理解已经全部完成了,想必应该可以轻松手搓一个属于自己的sdpa module。
Multi-Head Attention
MHA其实严格意义上算是对SDPA的一个升级版,相较于使用大矩阵进行QKV的运算,使用多个头来实现不同特征的融合可以提高模型的性能。而且也可以通过头之间的并行来实现计算加速。
MHA的核心其实就是如何进行分头计算,pytorch现在已经专门提供了多头注意力的计算Module,但是由于其中涉及到很多框架的相关设计,这里采用另一种实现,基于前面的pytorch的sdpa实现来实现MHA,这里的源码来自于github
MHA的官方代码是一个标准的pytorch module,其实从刚才的实现其实也可以知道SDPA算是MHA以及后面的GQA的子模块。
class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)
residual = q
# Pass through the pre-attention projection: b x lq x (n*dv)
# Separate different heads: b x lq x n x dv
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# Transpose for attention dot product: b x n x lq x dv
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
q, attn = self.attention(q, k, v, mask=mask)
# Transpose to move the head dimension back: b x lq x n x dv
# Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
q = self.dropout(self.fc(q))
q += residual
q = self.layer_norm(q)
return q, attn
Model parameters
依次来剖析如何进行计算的。首先是模型的参数定义部分:
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
因为SDPA的实现部分,没有提到参数矩阵的维度,但是在分析部分已经详细说明了各个参数的设计原因,其中$d_model$就是hidden_size。w_qs和w_ks的输出维度n_head * d_k就是前面的X。在上面我们说了V的输出维度应该是d_model,但是从实现上来看d_model显然不一定等于n_head * d_v,这是由于MHA的特性决定的,稍后在forword函数部分会详细说明一下。
关于定义部分实际上比较简单,没有什么特别多需要注意的地方。对于MHA,其实难点在于矩阵维度和计算的地方。
How data flow
首先看一下维度获取部分:
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)
residual = q
还是上面说的,这里的参数没太多需要注意的,主要是第二行,分别获取了batch_size,qkv的seq_len(这里还是假定三者相同)。
其次这里使用了q作为残差,这里实际上是源码命名的一个问题,在源码的MHA调用部分,实际上qkv三个是同一个输入,因此可以把qkv都看作x,也因此上面获取的len_q, len_k, len_v也是完全相同的。
# Pass through the pre-attention projection: b x lq x (n*dv)
# Separate different heads: b x lq x n x dv
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# Transpose for attention dot product: b x n x lq x dv
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
维度的转换确实是一个相当难理解的部分,在进行分头之前先对qkv都进行了对应的矩阵乘法,即:
q = self.w_qs(q); k = self.w_ks(k); v = self.w_vs(v)
之后是对其进行reshape操作来变成多头,并通过transpose将头维度和seqlen维度调换了一下,因此qkv的维度分别为(bs, n_head, seq_q, d_k),(bs, n_head, seq_k, d_k),(bs, n_head, seq_v, d_v)。虽然很乱,但是到这一步其实还是很好理解的。
接下来就是attention计算:(如果不把源码中的SDPA放出来可能会有人认为不同的实现会使得输入不同)
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9)
attn = self.dropout(F.softmax(attn, dim=-1))
output = torch.matmul(attn, v)
return output, attn
尽管实现上和torch的SDPA稍微存在差异,但是基本上运算过程完全一致,没有对头进行专门的处理。接下来我举一个例子来说明为什么会发生这种情况:
import torch
x = torch.randn((2,2,2,3))
y = torch.randn((2,2,3,2))
t = x[0][0]
h = y[0][0]
print((x@y)[0][0].equal(t@h))
# True
# x @ y:
# tensor([[[[-0.5371, 1.0102],
# [-0.0265, -0.2830]],
# [[ 2.1532, 0.2521],
# [-0.1639, -0.3164]]],
# [[[ 3.0916, 2.5055],
# [-5.6831, -2.0042]],
# [[ 0.1073, 0.5002],
# [ 0.0646, 0.2256]]]])
# t @ h:
# tensor([[-0.5371, 1.0102],
# [-0.0265, -0.2830]])
到这里其实应该就理解了,因为torch的矩阵乘法只对最后两个维度生效,所以完全可以忽略前面的bs维度和n_head维度。同理对于v的计算也是生效的。
# Transpose to move the head dimension back: b x lq x n x dv
# Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
q = self.dropout(self.fc(q))
q += residual
q = self.layer_norm(q)
return q, attn
接下来就是最后一步,残差运算和fc操作。前面的Attention操作我们得到了q(实际上就是注意力的结果),首先将其重新转换为(b, seq_len, n*dv)维度。之后再使用一个全连接层将n*dv维度转换为d_model维度。
可能有人疑惑最后这个fc是否有必要的存在,毕竟可以让n*dv == d_model,实际上,如果仅仅进行分头的计算,那么每个头只会拥有自己特征的信息,从而导致性能下降,因此最后使用这个output的一个核心点在于将不同头的特征进行处理。
至此,关于最基础的SDPA和MHA就已经完全理解,在此基础上自己实现应该也完全不是问题了。
Detailed Question Among SDPA and MHA
尽管对两者都有了详细的理解,但是仍然存在一些细节的问题需要知道。
- MHA和SDPA的计算复杂度哪个更高
如果不接触详细的矩阵计算,想必上述的过程应该是很难想通,但是既然学到现在,上述的计算问题就很简单了。由于数据和QKV参数矩阵的矩阵乘法两者是相同的,这里就直接进行一个省略计算,因此核心的计算过程在于$Q@K^T$和$attn@ V$
首先是SDPA的计算,我们从复杂的角度依次进行分析计算。假设Q和K均为$(S, X)$,V为$(S, D)$,头数为$H$,则计算复杂度为: $$\begin{align}O(SDPA)&= O(Q@K^T) + O(attn@ V) \ &= O({S}^2*X) + O({S}^2 * D)\end{align}$$
接下来是对于MHA的计算: $$\begin{align}O(MHA)&= O(Q@K^T) + O(attn@ V) + O(Q @ Output) \ &= O(H * {S}^2 * d_X) + O(H * {S}^2 * d_V) + O(d_V * H * S * D)\&=O(S^2X)+ O({S}^2 * D)+O(S{D}^2)\end{align}$$
可见,相较于SDPA,实际上MHA多出来了最后一个投影计算提高了计算次数(但是注意,计算复杂度是没有系数的)。在维度相同的情况下,两者的计算复杂度相同(这里假设$H*d_Y=D$)。因此也能证实很多营销号的内容其实严格意义上来说是对的。但是尽管添加了线性的计算量,MHA还是可以通过并行以及后续的GQA等操作来实现更加高性能的存储和计算。
- MHA如何实现并行
MHA可以通过不同头的并行计算从而提高计算速度,这里举一个llama项目中的实现来说明。由于篇幅问题就不详细说明了。
- KV-cache!
KVcache的理解说复杂也复杂,说简单也简单。简单在于一般来说的教程都告诉我们:token生成,KV只需要append新的token并计算新的部分就好了,但是Q为什么没有cache却没有多少人详细说明。 苏神提到了一嘴:缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA
由于这里只考虑了主流的自回归LLM所用的Causal Attention,因此在token by token递归生成时,新预测出来的第t+1个token,并不会影响到已经算好的k(s)≤t,v(s)≤t,因此这部分结果我们可以缓存下来供后续生成调用,避免不必要的重复计算,这就是所谓的KV Cache。
这里引用一下知乎里面的一篇回答为什么加速LLM推断有KV Cache而没有Q Cache?。简而言之就是说,对于Causal Attention情况下,通过式子推导的出来的隐藏层的值为$$\sum_{j=1}^tS_t(q_t\cdot k_j)v_j$$ 即只有k和q是不对称的,在计算的时候只有k和v需要之前的值。而对于q而言,由于新的计算只需要新的q参与,因此不需要使用q之前的值,所以只有kvcache。具体的公式推导如下:
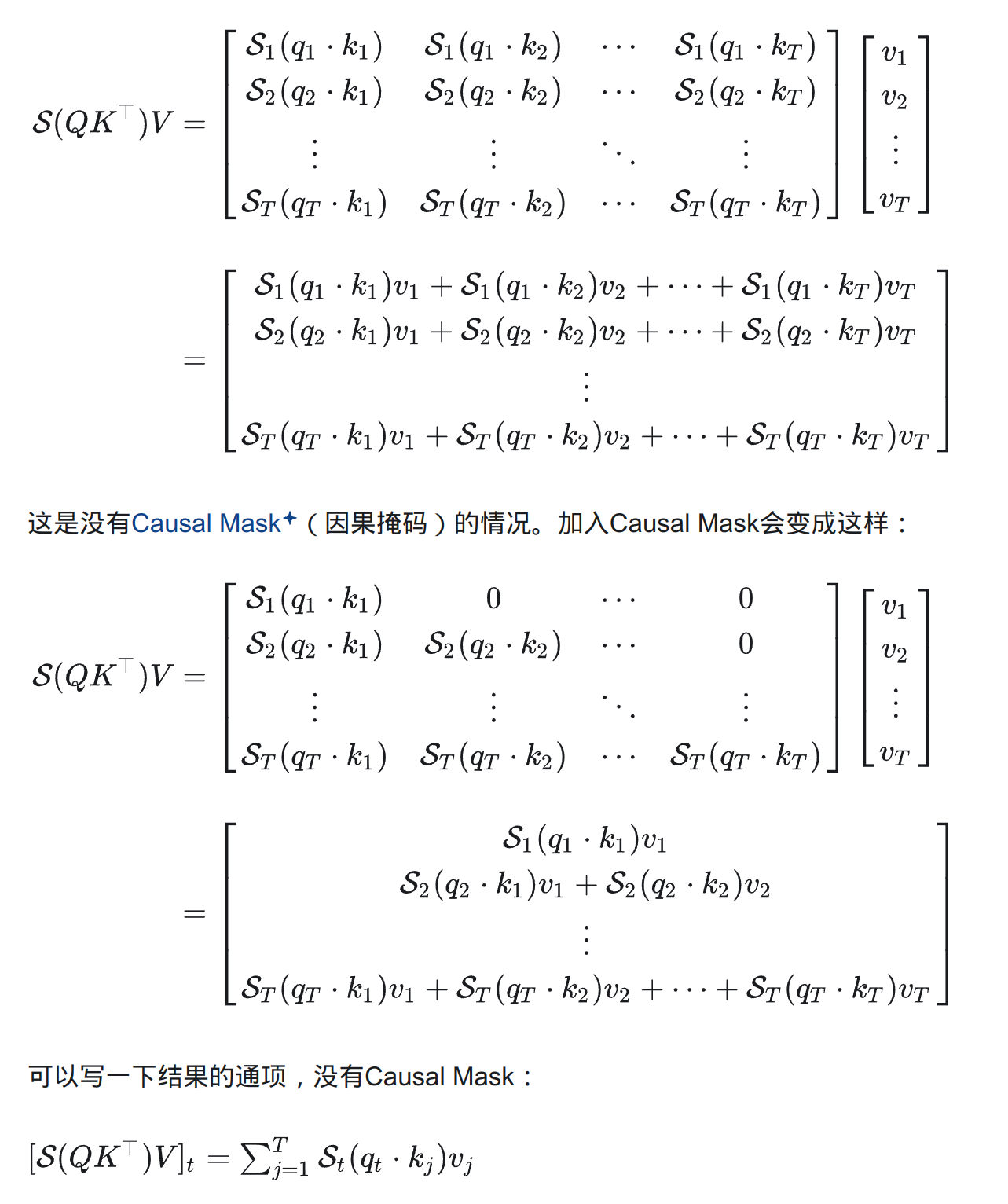
而对于没有Causal Mask的情况,由于需要未来的KV,因此无法得到。
GQA
Grouped-Query Attention的诞生是为了解决KV-cache问题的。下图是三种Attention的结构图:
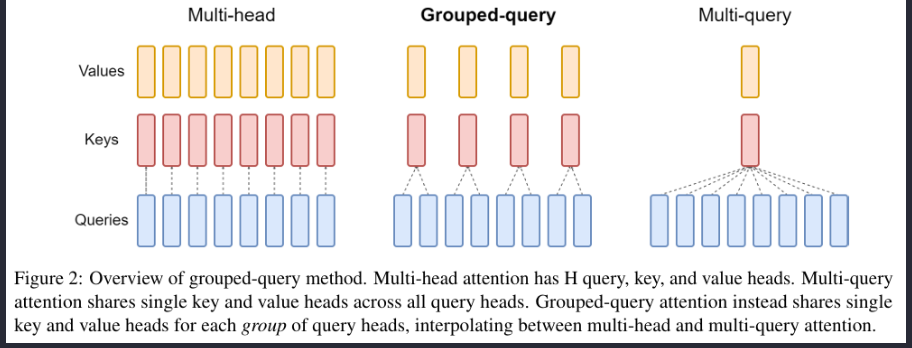
显然,通过减少k和v头的数量可以大幅度的减少kvcache的占用量(实际上是减少了维度),然而,这种压缩必然会带来性能的下降,为了均衡两者,现在更倾向于使用GQA来实现性能和占用的均衡。当然思路也很朴素,把head分成g个组。而在具体实施时,可以将不同组的KV放在不同的显卡上从而保证速度依旧很快。
就实现而言,不管是llama还是前面就提到的sdpa中都是很简单的一个操作:
key = key.repeat_interleave(query.size(-3)//key.size(-3), -3)
value = value.repeat_interleave(query.size(-3)//value.size(-3), -3)
只需要在head维度进行q//v倍数的复制即可。
由于实现和原理相对来说都不复杂,在此就不多说明了。
MLA(Multi-Latent Attention)
开源模型的发展速度还是相当快的,从GPT再到llama再到deepseek,基本上是一个不断迭代提升的过程,相较于GPT的MHA再到llama的GQA再到现在deepseek的MLA,基本上是一个不断递进发展的过程。(但是相较于前面的实现,MLA的图解和公式确实丑陋了一点)
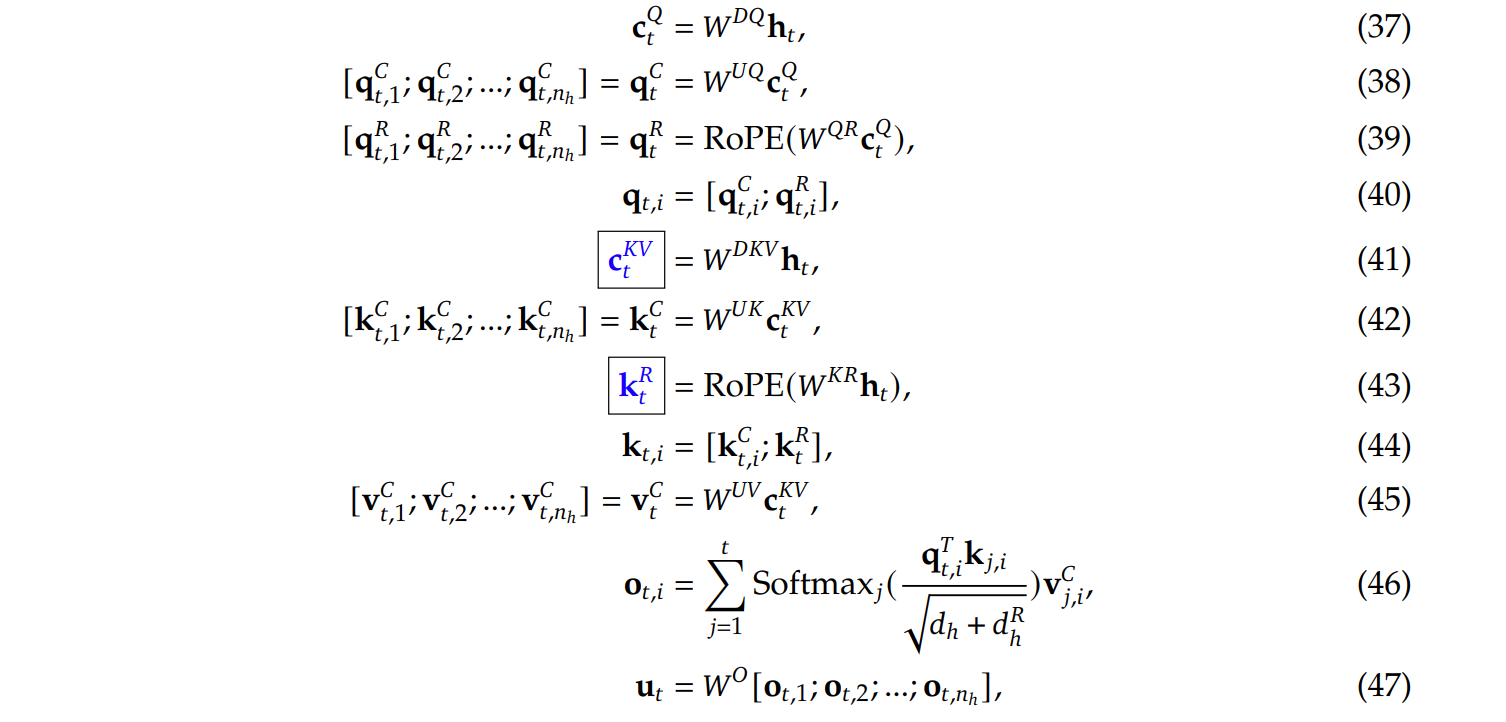
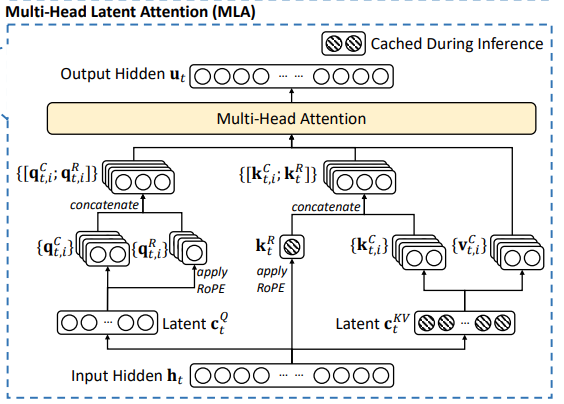
这两张图都算是deepseekv2论文中的内容,看来还是因为性能好才被大家解读的。
首先大致理解一下第二张图中的内容。对于输入的隐藏层数据h,首先降维到c(区分为q和kv的),之后在q的部分多出来一部分进行rope操作,同理,对于k也进行rope操作,而对于c的kv部分,经过kv矩阵乘法之后在进行接下来的部分。(说实话,从这个角度理解的话其实也并不复杂,说到底将上面的公式翻译下来也就这几步):
class MLA(nn.Module):
"""
Multi-Headed Attention Layer (MLA).
Attributes:
dim (int): Dimensionality of the input features.
n_heads (int): Number of attention heads.
n_local_heads (int): Number of local attention heads for distributed systems.
q_lora_rank (int): Rank for low-rank query projection.
kv_lora_rank (int): Rank for low-rank key/value projection.
qk_nope_head_dim (int): Dimensionality of non-positional query/key projections.
qk_rope_head_dim (int): Dimensionality of rotary-positional query/key projections.
qk_head_dim (int): Total dimensionality of query/key projections.
v_head_dim (int): Dimensionality of value projections.
softmax_scale (float): Scaling factor for softmax in attention computation.
"""
def __init__(self, args: ModelArgs):
super().__init__()
self.dim = args.dim
self.n_heads = args.n_heads
self.n_local_heads = args.n_heads // world_size
self.q_lora_rank = args.q_lora_rank
self.kv_lora_rank = args.kv_lora_rank
self.qk_nope_head_dim = args.qk_nope_head_dim
self.qk_rope_head_dim = args.qk_rope_head_dim
self.qk_head_dim = args.qk_nope_head_dim + args.qk_rope_head_dim
self.v_head_dim = args.v_head_dim
if self.q_lora_rank == 0:
self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
else:
self.wq_a = Linear(self.dim, self.q_lora_rank)
self.q_norm = RMSNorm(self.q_lora_rank)
self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim)
self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim)
self.kv_norm = RMSNorm(self.kv_lora_rank)
self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim))
self.wo = RowParallelLinear(self.n_heads * self.v_head_dim, self.dim)
self.softmax_scale = self.qk_head_dim ** -0.5
if args.max_seq_len > args.original_seq_len:
mscale = 0.1 * args.mscale * math.log(args.rope_factor) + 1.0
self.softmax_scale = self.softmax_scale * mscale * mscale
if attn_impl == "naive":
self.register_buffer("k_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.qk_head_dim), persistent=False)
self.register_buffer("v_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.v_head_dim), persistent=False)
else:
self.register_buffer("kv_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.kv_lora_rank), persistent=False)
self.register_buffer("pe_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.qk_rope_head_dim), persistent=False)
def forward(self, x: torch.Tensor, start_pos: int, freqs_cis: torch.Tensor, mask: Optional[torch.Tensor]):
"""
Forward pass for the Multi-Headed Attention Layer (MLA).
Args:
x (torch.Tensor): Input tensor of shape (batch_size, seq_len, dim).
start_pos (int): Starting position in the sequence for caching.
freqs_cis (torch.Tensor): Precomputed complex exponential values for rotary embeddings.
mask (Optional[torch.Tensor]): Mask tensor to exclude certain positions from attention.
Returns:
torch.Tensor: Output tensor with the same shape as the input.
"""
bsz, seqlen, _ = x.size()
end_pos = start_pos + seqlen
if self.q_lora_rank == 0:
q = self.wq(x)
else:
q = self.wq_b(self.q_norm(self.wq_a(x)))
q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)
q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
q_pe = apply_rotary_emb(q_pe, freqs_cis)
kv = self.wkv_a(x)
kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
if attn_impl == "naive":
q = torch.cat([q_nope, q_pe], dim=-1)
kv = self.wkv_b(self.kv_norm(kv))
kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)
k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1)
self.k_cache[:bsz, start_pos:end_pos] = k
self.v_cache[:bsz, start_pos:end_pos] = v
scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale
else:
wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size)
wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank)
q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim])
self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv)
self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2)
scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) +
torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale
if mask is not None:
scores += mask.unsqueeze(1)
scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x)
if attn_impl == "naive":
x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos])
else:
x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bsz, :end_pos])
x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:])
x = self.wo(x.flatten(2))
return x
尽管整体的代码非常混乱,充斥着各种lora、einsum、索引计算,对于理解整个过程无疑是增加了难度,因此我将按照论文的大致思路和对应的代码一步一步来。目前主要分为如下步骤:
- QKV降维
- Q旋转编码
- K旋转编码
- attention操作
QKV降维
QKV的降维实际上就是图中最底层的内容:

找一下源码中涉及到的相关内容:
def MLA():
def __init__():
...
# part of Q
if self.q_lora_rank == 0:
self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
else:
self.wq_a = Linear(self.dim, self.q_lora_rank)
self.q_norm = RMSNorm(self.q_lora_rank)
self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim)
# part of KV
self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim)
self.kv_norm = RMSNorm(self.kv_lora_rank)
self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim))
def forward():
...
# part of Q
if self.q_lora_rank == 0:
q = self.wq(x)
else:
q = self.wq_b(self.q_norm(self.wq_a(x)))
q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)
# part of KV
kv = self.wkv_a(x)
如果没有LoRA的相关知识的话建议先补一下LoRA知识,这样才知道为什么这样设计。LoRA是分为一个降维矩阵和升维矩阵,在这里体现的地方是下标_a和_b。对于q,在进行一次LoRA操作之后当即就恢复了,之后将q根据qk的head维度做了resize(注意,因为QK是先乘的,因此要求qk_head_dim相同是自然的)。然而对于kv,则没有直接升维,而是先保存了降维版本。
Q旋转编码
接下来抛开KV不谈,我们讨论一下Q是怎么增加旋转编码的。
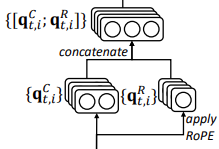
从图中来看实际上就是拆成两部分之后把一部分拿过来加入了旋转编码。代码如下:
def MLA():
def __init__():
...
def forward():
...
q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
q_pe = apply_rotary_emb(q_pe, freqs_cis)
...
if attn_impl == "naive":
q = torch.cat([q_nope, q_pe], dim=-1)
实际上就是拆开转一下又放回去了。
K旋转编码和拼接
K的旋转编码以及拼接倒是没那么简单,但是也不复杂:
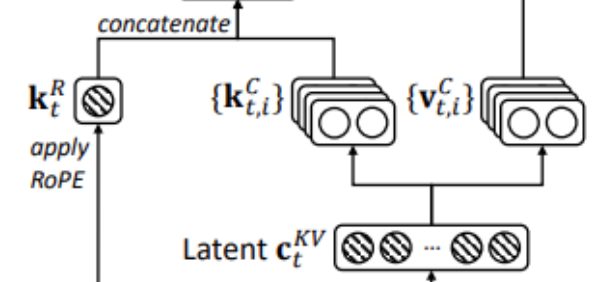
看看源码:
def MLA():
def __init__():
...
def forward():
...
kv = self.wkv_a(x) # 前面提到了
kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis)
...
if attn_imple == "naive":
...
kv = self.wkv_b(self.kv_norm(kv))
kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)
k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1)
k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1)
self.k_cache[:bsz, start_pos:end_pos] = k
self.v_cache[:bsz, start_pos:end_pos] = v
对于KV部分,前面我们通过降维得到了kv,之后将kv分成了两部分(降维矩阵相同),看似是两部分(这里是把降维后的latent空间的数据进行旋转编码,和q有差别的)。因此自然的,对用用rope的k_pe进行旋转编码。
之后在attn中,降维的一部分拿出去做rope了,剩下的不用管,直接进行升维得到k和v,此时得到的kv里包含了k的没有rope的部分和v的部分,进行split之后进行把k_nope和k_pe合并即可。
attention操作
最后就是熟知的attention操作了:
def MLA():
def __init__():
...
def forward():
...
scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale
...
x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos])
...
x = self.wo(x.flatten(2))
这里用的爱因斯坦积操作,实际上还是矩阵乘法和各种reshape的集合,这里我用claude转换为正常操作,自己理解一下就好了(从这个角度来看的话高维度矩阵乘法确实不如直接利用爱因斯坦积实现):
# ----- 第一个操作
# 原始形状:
# q: [batch_size, seq_len, num_heads, head_dim]
# k_cache: [batch_size, total_len, num_heads, head_dim]
# 等价矩阵乘法:
# 1. 调整维度顺序
q_reshaped = q.permute(0, 2, 1, 3) # [b, h, s, d]
k_reshaped = k_cache[:bsz, :end_pos].permute(0, 2, 3, 1) # [b, h, d, t]
# 2. 批量矩阵乘法
scores = torch.matmul(q_reshaped, k_reshaped) * self.softmax_scale # [b, h, s, t]
# 3. 恢复原始维度顺序
scores = scores.permute(0, 2, 1, 3) # [b, s, h, t]
# ----- 第二个操作
# 原始形状:
# scores: [batch_size, seq_len, num_heads, total_len]
# v_cache: [batch_size, total_len, num_heads, head_dim]
# 等价矩阵乘法:
# 1. 调整维度顺序
scores_reshaped = scores.permute(0, 2, 1, 3) # [b, h, s, t]
v_reshaped = v_cache[:bsz, :end_pos].permute(0, 2, 1, 3) # [b, h, t, d]
# 2. 批量矩阵乘法
x = torch.matmul(scores_reshaped, v_reshaped) # [b, h, s, d]
# 3. 恢复原始维度顺序
x = x.permute(0, 2, 1, 3) # [b, s, h, d]
# ----- 第三个操作
x = self.wo(x.flatten(2)) # flatten最后两个维度 [b, s, h*d]
至此,就算是完全理解了MLA的过程了,但是这里依旧存在很多细节需要说明,接下来依次说明吧。
注意:这里有一个细节比较怪,在源论文公式实现中旋转编码是对降维后的q进行的,但是代码并不是,难不成两者的效果相同?好像得验证一下。
RoPE
如何RoPE
MLA做出这种怪异结构的一个重要原因就是需要使用RoPE,位置编码已经在很多地方证明有效性了,而其中的RoPE也是佼佼者,因此将RoPE应用其中是需要的。至于为什么这样做,可以详细参考苏神的文章:缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA
首先,位置编码的提出是为了解决大预言模型的外推性问题,如果推理时的token数量和训练时的token数量不同,会导致性能下降的问题,RoPE的提出很好的解决了这个问题。当然,如果从头开始理解位置编码的话可能需要花相当大的功夫,这里忽略一下众多的位置编码种类和对应的变体,着重说明一下RoPE的计算过程和优化实现,从而对MLA有更好的理解。
原理和计算
为了知道RoPE的计算方式,我觉得还是有必要知道RoPE的原理。对于RoPE,其是一个相对位置编码,对于长度分别为m,n的q和k,相较于对绝对的位置进行编码,考虑到两者最后是需要进行矩阵乘法的,较好的方式其实是获得token间的相对位置关系。同时,考虑到seqlen的变化性,最好的方式是选择一个可以推广很长的位置编码方式,这种情况下,使用三角函数是一个不错的选择,此外,距离越远的相关性会弱一点,因此还需要衰减性,基于上述的一些性质,就有了RoPE,其函数图如下:
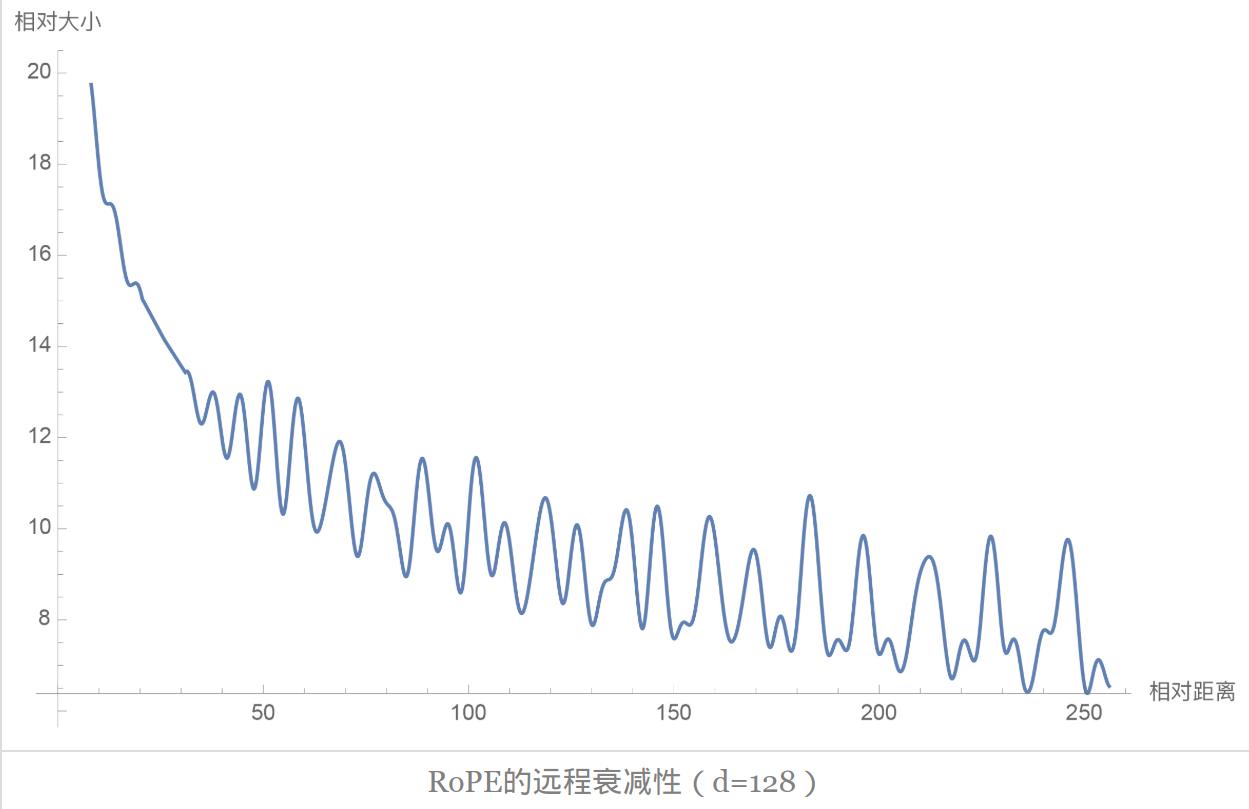
我们知道hidden_state在完成q和k参数矩阵乘法之后即可得到对应的注意力矩阵,其表示token之间的注意力值,大小为$(seq_len, seq_len)$,RoPE简而言之就是通过增加token之间的位置关系,自然而然最好的添加方式就是在进行qk参数矩阵乘法之后,注意力计算之前。那么看一下如何实现计算,首先从二维角度引入:
$$\begin{equation} \boldsymbol{f}(\boldsymbol{q}, m) =\begin{pmatrix}\cos m\theta & -\sin m\theta\ \sin m\theta & \cos m\theta\end{pmatrix} \begin{pmatrix}q_0 \ q_1\end{pmatrix}\end{equation}$$
当然,对应的k也是这种计算方式,因此引入RoPE后,整个注意力矩阵为:
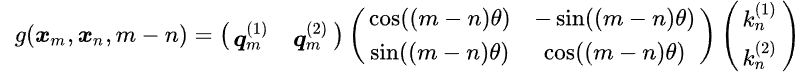
如果还有高中和大学知识的话,上述的计算过程实际上就是一个矩阵的旋转运算,在二维的情况下可以通过上述公式计算,但是对于多维情况,其计算方式如下:
$$\begin{equation}\scriptsize{\underbrace{\begin{pmatrix} \cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \ \sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \ 0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \ 0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \ \end{pmatrix}}{\boldsymbol{\mathcal{R}}m} \begin{pmatrix}q_0 \ q_1 \ q_2 \ q_3 \ \vdots \ q{d-2} \ q{d-1}\end{pmatrix}}\end{equation}$$
令人悲伤的是,这个东西需要占用大量的存储,难道说就不可用了吗?还是之前学过的三角函数运算,这个运算如果拆成两两运算的话,实际上可以变成下面的形式:
$$\begin{equation}\begin{pmatrix}q_0 \ q_1 \ q_2 \ q_3 \ \vdots \ q_{d-2} \ q_{d-1} \end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0 \ \cos m\theta_0 \ \cos m\theta_1 \ \cos m\theta_1 \ \vdots \ \cos m\theta_{d/2-1} \ \cos m\theta_{d/2-1} \end{pmatrix} + \begin{pmatrix}-q_1 \ q_0 \ -q_3 \ q_2 \ \vdots \ -q_{d-1} \ q_{d-2} \end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0 \ \sin m\theta_0 \ \sin m\theta_1 \ \sin m\theta_1 \ \vdots \ \sin m\theta_{d/2-1} \ \sin m\theta_{d/2-1} \end{pmatrix}\end{equation} $$ 到这里就好理解多了,但是在实现的时候,我们一般不是这样实现的,在二维的情况下,可以通过拆分变成一个计算公式,如果学过复数的运算的话,可以发现其实运算方式是一样的,详细可以参考这一篇:旋转之一 - 复数与2D旋转
至此就可以着手于实现RoPE的计算了,这里我们拿Llama中的最小的RoPE实现(当然也算是我做了更改和注释):
def naive_rope(
x: torch.Tensor,
theta: float = 10000.0,
) -> Tuple[torch.Tensor, torch.Tensor]:
dim = x.shape[-1]
seq_len = x.shape[-2]
# get the shape of x (ignore the head dimension).
# x: [batch_size, seq_len, dim]
x_ = x.float().reshape(*x.shape[:-1], -1, 2)
# x_: [batch_size, seq_len, dim//2, 2]
x_ = torch.view_as_complex(x_)
# pack neibored element into a complex
# x_: [batch_size, seq_len, dim//2, 1]. eg: tensor([(1.6116-0.5772j), ...]
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
t = torch.arange(seq_len , device=freqs.device)
freqs = torch.outer(t, freqs).float().cuda()
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
# get rotate angle
xq_out = torch.view_as_real(x_ * freqs_cis).flatten(1)
# do rotate
return xq_out.type_as(x)
MLA again
对RoPE理解之后就是最后一步了,我们得解决一下公式和实现上的问题,从矩阵运算的角度分析一下,理论上: $$RoPE(x@down@up) != RoPE(x)@down@up$$
编码测试一下事实也确实不同,那么为什么这样做了,说来好笑,在deepseek-v3的参数设置中,负责控制q降维的一个参数q_lora_rank设置为0,这使用的q实际上只是进行了一个线性变化而没有实现lora,而论文中是将这个的输出视为c的,才出现了这样的效果。但是不管怎么说这里都算是一个非常奇怪的理解的地方。当然我们就不把更多功夫花在这里了。
关于RoPE能否加入MLA,实际上也是一个问题,对于正常的推理,由于RoPE是跟位置有关的,如果只是简单的采用一个W进行处理的话,两个矩阵运算是可以合并保存从而提高推理速度的,但是加入RoPE之后,其与相对位置有关,因而无法直接实现矩阵的合并,因此才有了多出来一部分做RoPE的操作,具体的还是看苏神的MLA文章会更好一点:
deepseek技术解读(1)-彻底理解MLA(Multi-Head Latent Attention)
至此,关于Attention的内容就全部结束了,从最开始的SDPA再到MHA到现在的MLA,实际上还是围绕着显存做文章的,不过估计接下来的很长一段时间,围绕计算速度、显存相关的工作想必还是会有很多吧。
FlashAttention
这个基本是现在Attention Kernel最常用的一个实现了,其原理说复杂也不复杂,但是论文的一堆伪代码可以直接把人干碎,因此要是想要好好理解还是需要花一点功夫的。
首先,大模型的推理目前是分为两个阶段的,即预填充阶段和解码阶段,令人悲伤的是,两者其实存在较大的差异,对于预填充阶段,由于短时间会出现大量的Token用于计算KV(以及Q),因此这个过程的瓶颈是计算瓶颈。而解码阶段则是存储瓶颈,需要来回读取KVcache来生成下一个token。
FlashAttention的目标在于尽可能地减少内存的读取,对于传统的Attention(这里就不给出Attention的计算公式了),一个严重的问题是,要是多轮次计算,需要先计算$QK^T$之后计算$Softmax$最后还需要算一个$attn@ V$,使得整个过程的计算时间主要卡在内存读取上了(更何况最基础的Softmax还需要读取2~3遍$attn$矩阵)
在说FlashAttention之前得先说明一下softmax的计算公式,为了防止溢出(对于BF16精度,只要x>11就会导致溢出),一般来说要对每个数值x减去最大值,所以公式如下:

图中是一个safe-softmax的实现,可以看出,要是想计算一个softmax,其需要读取三次内存,首先获取最大值,之后计算和,最后更新每个数值,这谁受得了啊,因此就有了online-softmax,其原理也很简单,对于计算最大值,其实可以解耦通过如下方式解耦一下:
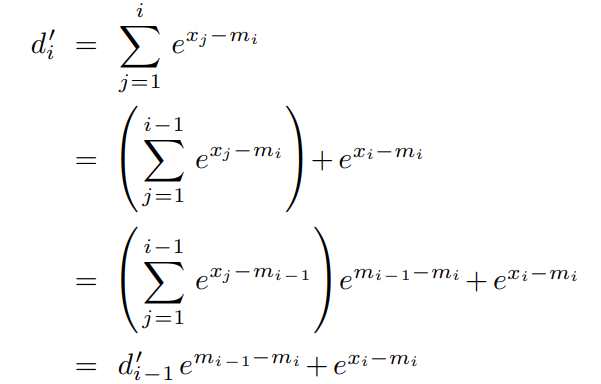
因此可以同时计算得到最大值和求和,从而将读取次数从3次降到了两次,这里我提供一下CUDA代码:
struct __align__(8) MD { float m; float d; };
// Warp Reduce for Online Softmax
template<const int kWarpSize = WARP_SIZE >
__device__ __forceinline__ MD warp_reduce_md_op(MD value) {
unsigned int mask = 0xffffffff;
#pragma unroll
for(int stride = kWarpSize >> 1; stride >= 1; stride >>= 1) {
MD other;
other.m = __shfl_xor_sync(mask, value.m, stride);
other.d = __shfl_xor_sync(mask, value.d, stride);
bool value_bigger = (value.m > other.m);
MD bigger_m = value_bigger ? value : other;
MD smaller_m = value_bigger ? other : value;
value.d = bigger_m.d + smaller_m.d * __expf(smaller_m.m - bigger_m.m);
value.m = bigger_m.m;
}
return value;
}
template <const int NUM_THREADS = 256 / 4>
__global__ void online_safe_softmax_f32x4_pack_per_token_kernel(float *x, float *y, int N)
{
// reference: https://arxiv.org/pdf/1805.02867 (Online normalizer calculation for softmax)
int local_tid = threadIdx.x;
int global_tid = (blockIdx.x * NUM_THREADS + local_tid) * 4;
const int WAPR_NUM = NUM_THREADS / WARP_SIZE;
int warp_id = local_tid / WARP_SIZE;
int lane_id = local_tid % WARP_SIZE;
// compare local max value
float4 val = FLOAT4((x)[global_tid]);
float local_m = fmaxf(fmaxf(val.x, val.y), fmaxf(val.z, val.w));
float local_d = __expf(val.x - local_m) + __expf(val.y - local_m) + __expf(val.z - local_m) + __expf(val.w - local_m);
MD local_md = {local_m, local_d};
MD res = warp_reduce_md_op<WARP_SIZE>(local_md);
__shared__ MD shared[WAPR_NUM];
if (lane_id == 0) shared[warp_id] = res;
__syncthreads();
// do block reduce
if (local_tid < WARP_SIZE)
{
MD block_res = shared[local_tid];
block_res = warp_reduce_md_op<WAPR_NUM>(block_res);
if (local_tid == 0) shared[0] = block_res;
}
__syncthreads();
// write back
MD final_res = shared[0];
float d_total_inverse = __fdividef(1.0f, final_res.d);
if (global_tid < N)
{
float4 reg_y;
reg_y.x = __expf(val.x - final_res.m) * d_total_inverse;
reg_y.y = __expf(val.y - final_res.m) * d_total_inverse;
reg_y.z = __expf(val.z - final_res.m) * d_total_inverse;
reg_y.w = __expf(val.w - final_res.m) * d_total_inverse;
FLOAT4((y)[global_tid]) = reg_y;
}
}
为了保证一次计算结束,需要保存一下当前块的最大值,从而方便恢复。(这个当时写出来对我来说是真的难)。首先对于每个数字,都记录其e值和最大值,则在遇到新的最大值可以通过简单的除法再乘法恢复。这里用的是一个洗牌操作进行实现,有点类似归约求和的步骤,每次按一个stride两两进行求和和比较大小,如果遇到更大的就恢复一下,否则求和即可。之后外部对多个block做上述操作之后对每个block再进行一次,从而计算得到最大值和和,然后对每个值计算softmax即可。
那么问题来了,尽管上述实现了online-softmax并直接缩短到了2-pass操作,但是要知道attention的一整个操作都是1-pass的,这确实是一个很神奇的地方,接下来就可以详细看一下flashattention的原理和实现了。(源码过于夸张了)
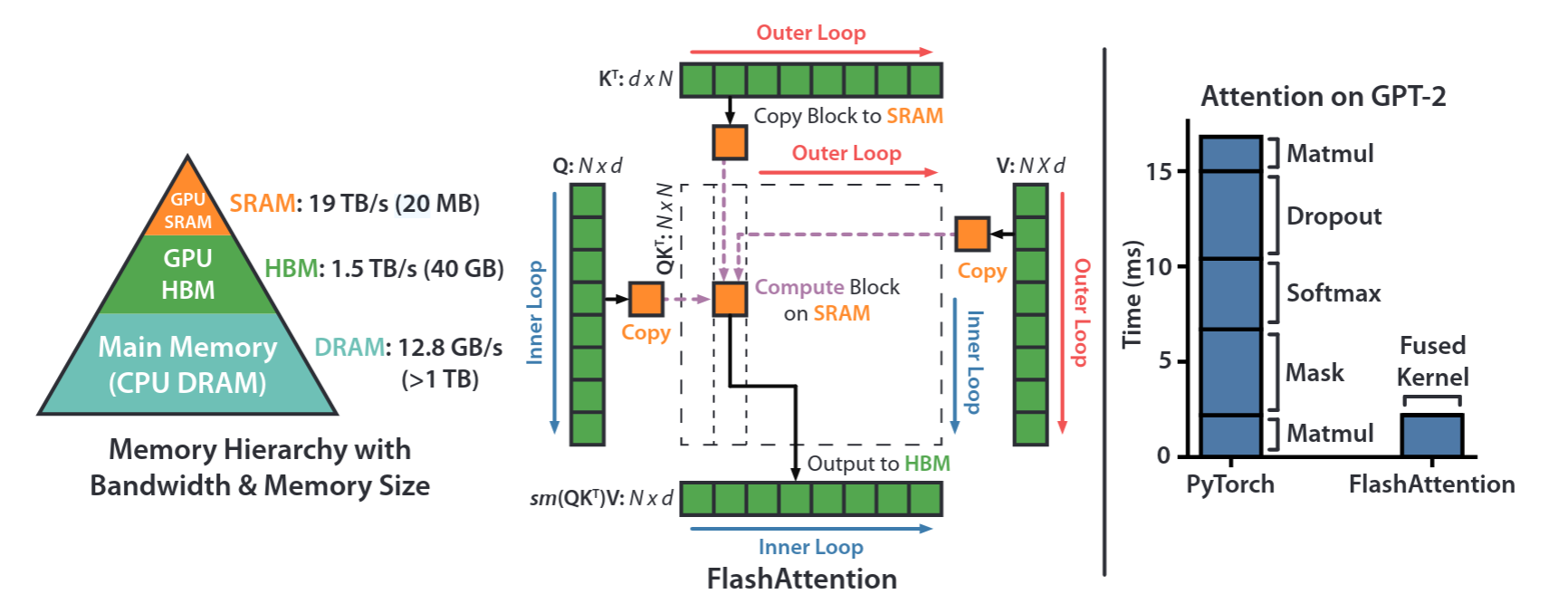
核心就是上面的图,每次把QKV的block取出来之后直接计算就可以得到结果了,问题在于Softmax的max和sum操作是必须要所有seqlen参与的,这是如何实现的?接下来继续看。根据上面说到的Softmax操作,我们可以得到高级的Attention操作:

首先计算QK并不断更新当前的最大值和和,之后计算每个token的softmax值并乘以V,最后写回。这个过程整体而言是一个3-pass的attention操作了(最原始attention可以有8-pass读取)。有时候我们看起来无法提升的操作在大佬眼里还有更夸张的提升效果:

这个东西哈人坏了,我觉得得好好消化一下。逐行讲解一下。
- init 输入为Q K V以及SRAM的大小M
- line1:根据SRAM的大小和输入向量维度决定两个值$B_r$和$B_c$
- line2:初始化一个数组空间O,N维向量的l和m分别来记录每个positon的EXP和和和最大值
- line3&line4:将QKV和O矩阵进行分块:
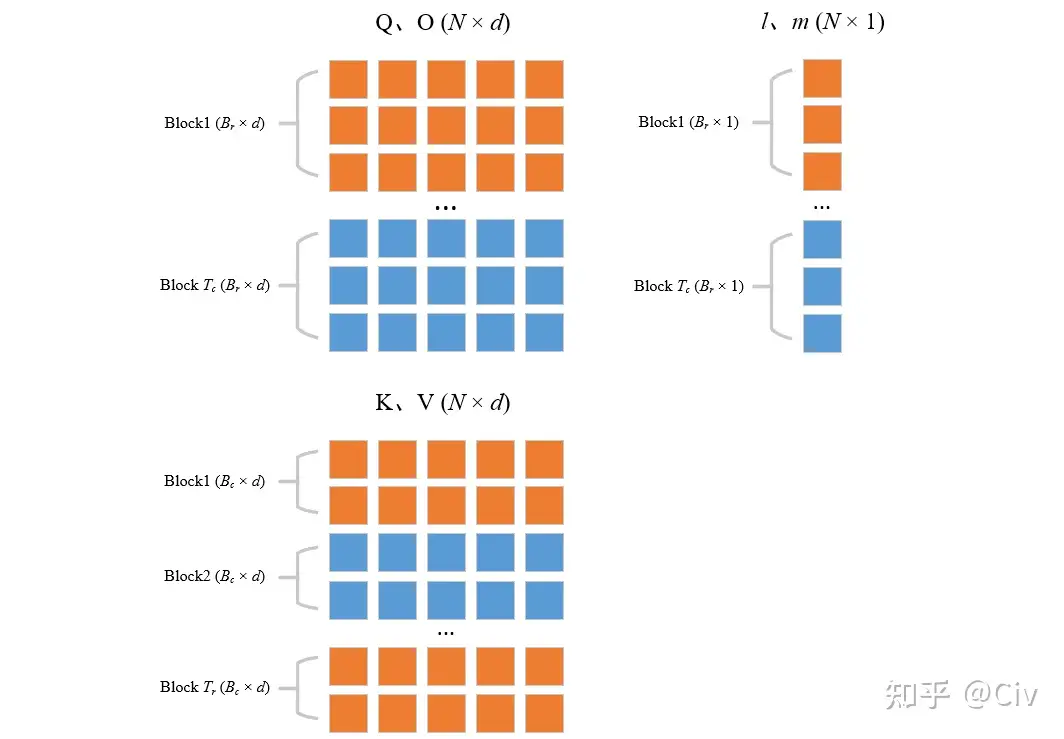
-
line5:遍历KV
-
line6:将当前的KV读写到SRAM
-
line7:遍历Q,O,l,m
-
line8:将当前遍历的Q,O,l,m读入SRAM
-
line9:将当前的QK计算attention Score S:
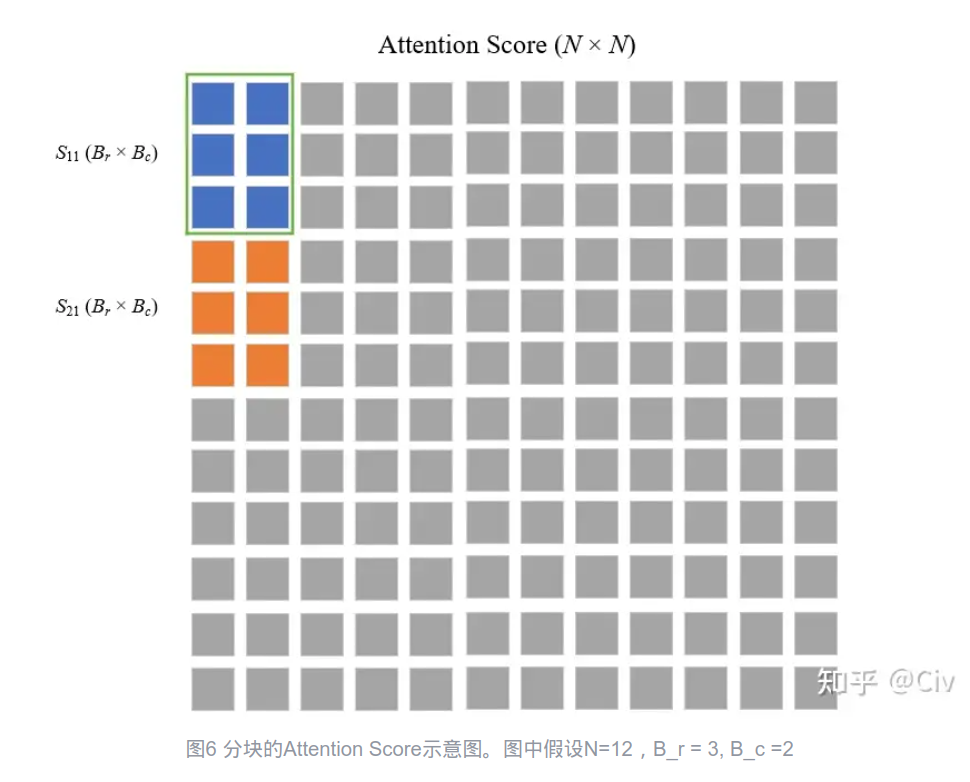
image-20250220165651976 -
line10:对于S,得到每行的最大值,并计算指数项和求和
-
line11:利用前面的onlinesoftmax方法更新m和l
-
line12:这一行比较复杂。通常来说attention的softmax是对列进行的,因此行与行之间是没有计算上的依赖或者冲突的。
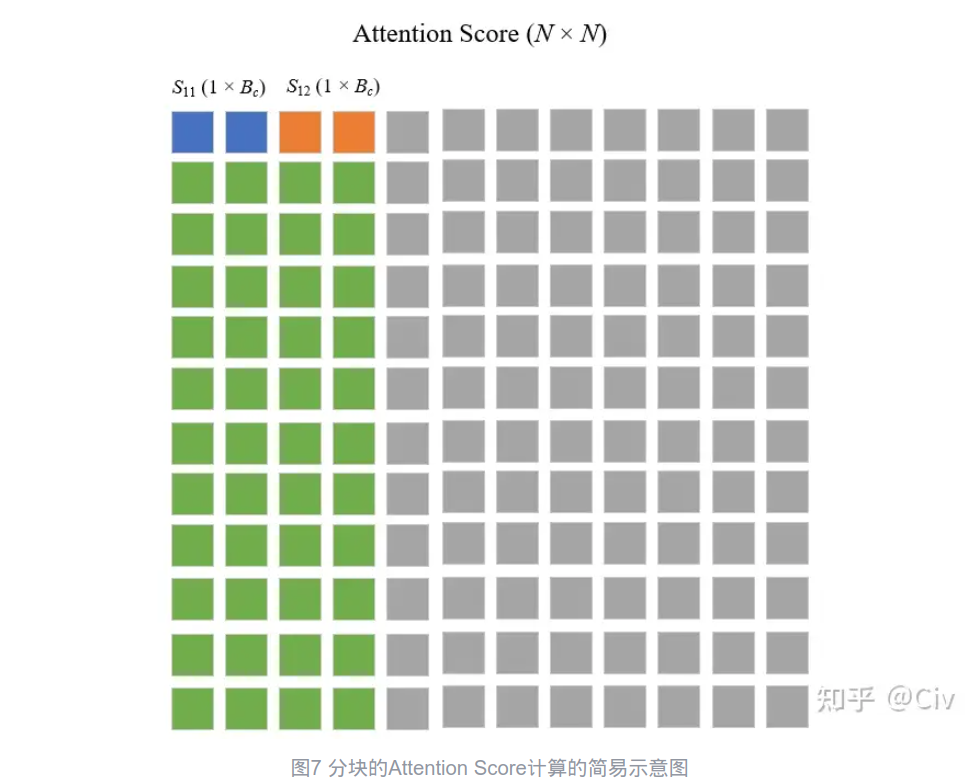
image-20250220170732732 对于这每一列的attention score,可以先计算局部softmax,并把和和最大值记录一下。接着处理$S_{12}$同样计算局部softmax并不断更新SM值。完成之后直接尝试更新输出O1,这个也很简单,因此softmax的计算可以同样可以利用前面记录的值进行恢复。
-
line13:更新l和m即可
-
-
上述是从伪代码的角度分析的,实际上对于FlashAttention而言,其类似Online-Softmax的一个关键在于如何减少递归关系:
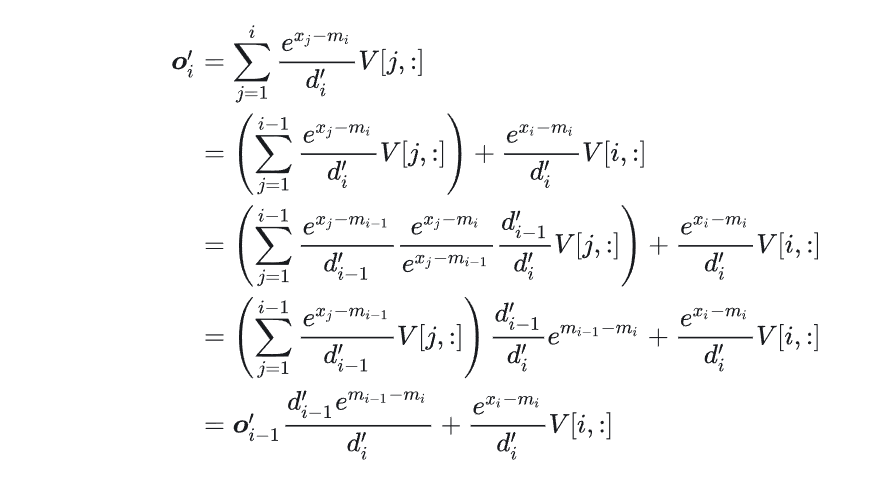
实际上发现O的计算根本不依赖全局的m和全局的l,因此可以变成

然而,FlashAttention的还对反向传播也做了优化,复杂度想较于上面进一步提升了,整体而言确实比较哈人。
除此之外还有FlashDecoding, FlashAttention2,Memory-Efficient Attention