CUDA指令集

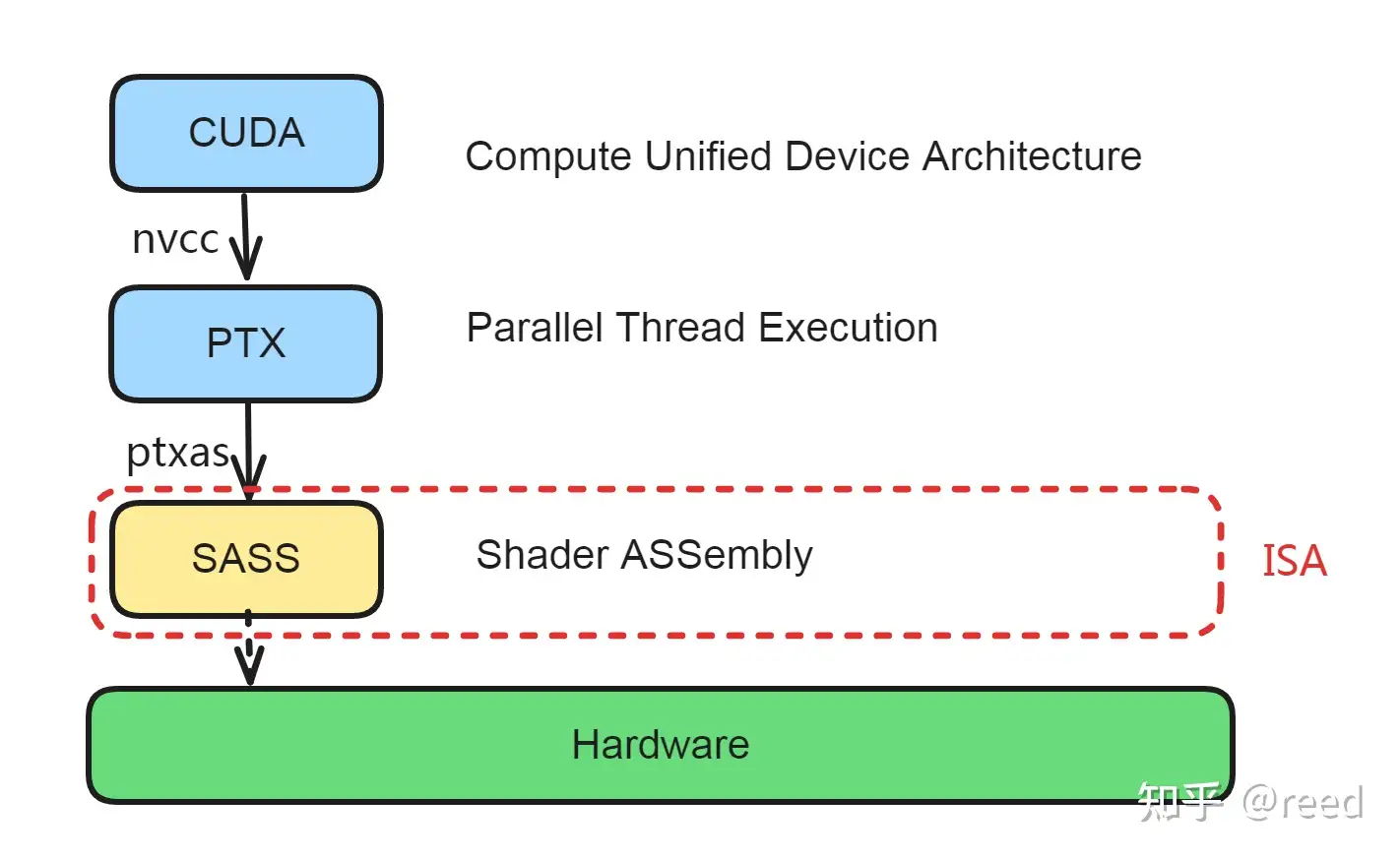
对于NVidia GPU而言，其软件部分的核心语言为CUDA（Compute Unified Device Architecture），硬件架构的指令在不同代际是不同的（如Tesla，Fermi, Keper, Maxwell, Pascal, Volta, Turing, Ampere, Hopper，Blackwell）

从CUDA编写到硬件计算的总体过程如下：

寄存器

对于Nvidia的GPU，其寄存器有：通用寄存器、特殊寄存器、Predicate寄存器、Uniform寄存器。

Load-Store架构

考虑到GPU每个计算单元的复杂程度，其架构实际上类似于RISC的Load-Store架构，所有计算类指令的原操作数和目的操作数都必须是寄存器，内存和寄存器的通讯通过独立的Load和Store指令完成。NVidia Ampere及其之前的GPU架构基本符合Load Store架构的定义（有一点不符合的是常量内存），且为了提高内存的访问效率和数据局部性，内存层次比CPU架构多了不少。当然，这里就涉及到之前CUDA编程的内容了，不是今天的重点。整体的Load和Store指令的操作数情况如下：

指令	类型	目标操作位置	源操作位置
LDG	Load	寄存器	全局内存
STG	Store	全局内存	寄存器
LDS	Load	寄存器	共享内存
STS	Store	共享内存	寄存器
LDL	Load	寄存器	局部内存
STL	Store	局部内存	寄存器
LDSM	Load	寄存器	共享内存
非Load/Store指令	算数指令	寄存器	寄存器

基于这样一个架构，会有诸多优势比如：指令集简单直观、流水线设计高效、编译器优化、寄存器利用高效、指令格式清晰、适合并行处理

寄存器表达的程序状态机

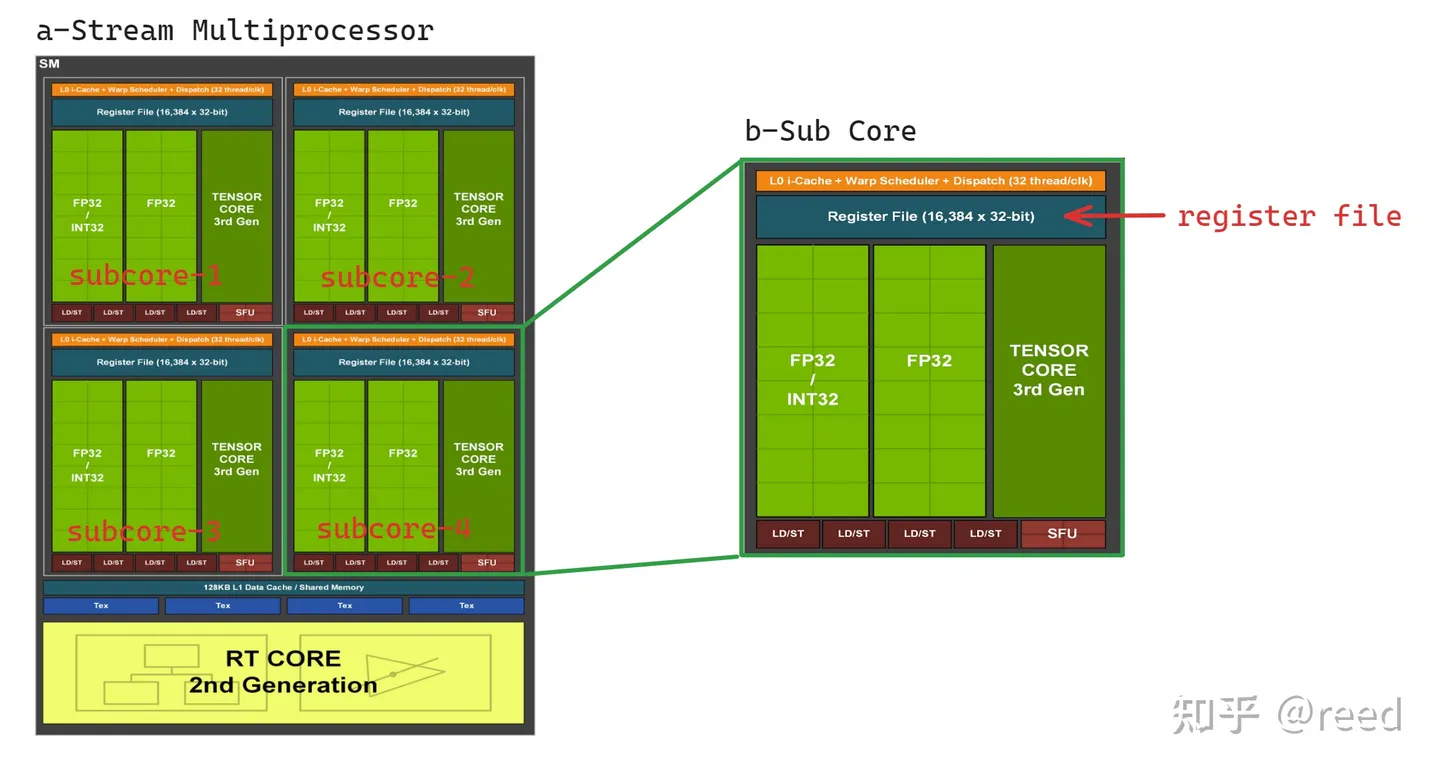
图为Ampere架构的SM，对于一个SM包含4个subcore，其中每个subcore还包含着16384个寄存器（通用寄存器），GPU的一个调度单位是warp，每个warp包含32个lane并共享着相同的代码，所以寄存器数量对应的每个lane分到512组寄存器，因此初步来看整体的划分如下：

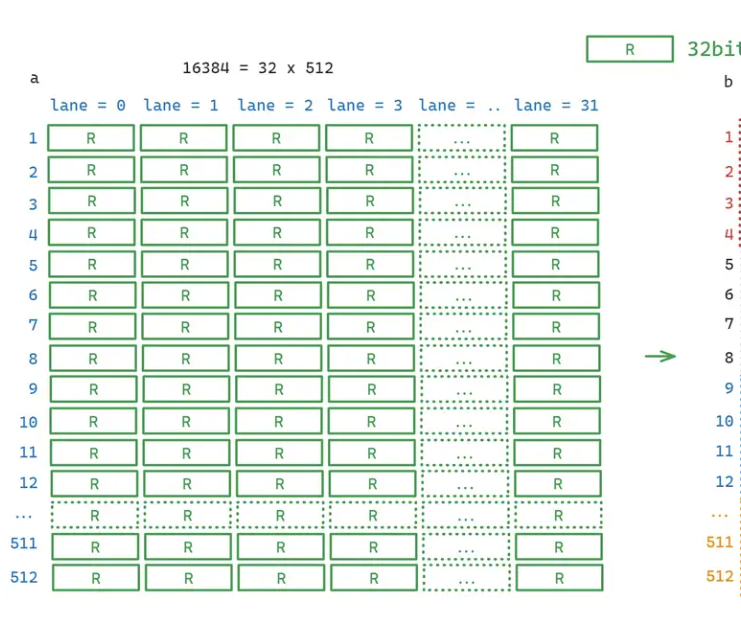
当SM执行kernel时，寄存器分给不同的warp，当每个lane分配4个寄存器的时候情况如图（对应R0~3）：

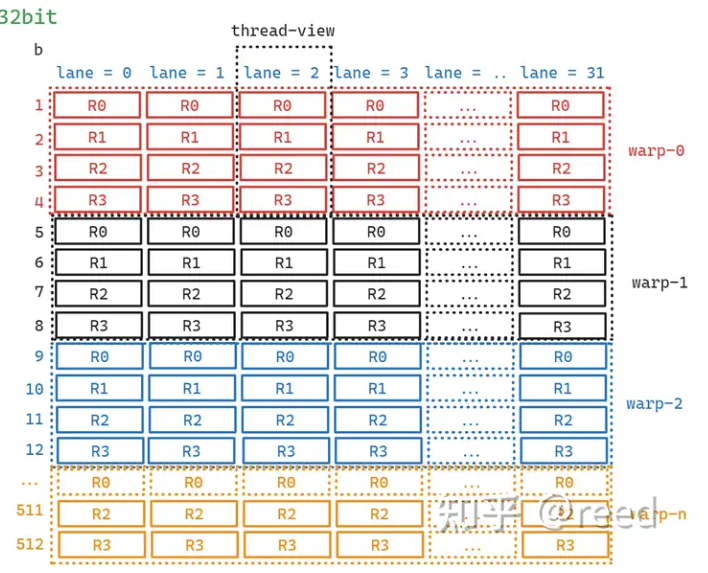
这种寄存器分配模式构成了CUDA中最重要的延迟隐藏机制，那就是程序的执行状态都在寄存器中被记录和表示，warp调度单元选择一个可以执行的单元，利用执行单元（如图1中的FP32单元）读取特定warp对应的寄存器中的数据，将结果写入到这些寄存器中。如某个warp遇到了Load指令需要较多cycle才能获取到数据，而warp调度器则可以切换到其他数据已经ready需要进行计算任务的warp执行，即换一组寄存器表的状态即可（类似于CPU的线程调度）。如此便做到了执行单元只有一份，但是表达程序运行状态的存储单元却有多份，并且这种切换执行是十分轻量的，其和CPU中的超线程是类似的：一份执行单元，多份寄存器状态。通过warp切换来达到延迟隐藏的目的。物理硬件上寄存器文件一般使用SRAM（static random access memory）实现。

接下来就是对各种寄存器的了解

通用寄存器

最快最通用，可读可写，位宽只有32bit一个线程最多支持255各寄存器。由于寄存器的位宽为32bit，有时候算法需要更宽的数据存储结构时，则采用连续的多个寄存器组来完成，在SASS编码中只体现首寄存器编号，其余的寄存器不体现在编码中。如F2F.F64.F32 R4, R2; 表示32bit浮点数到64bit浮点数的类型转换(float to float: float32 to float64)，其中目标寄存器需要使用两个连续的寄存器R4R5来存储double值，源寄存器R2存储float值。另外约定R255寄存器为常零寄存器，在SASS中表示为RZ（Register ZERO）。

R0, R1, R2, R3, ..., R251, R252, R253, R254, R255(RZ)

特殊寄存器

一般只读用于保存重要信息，用于标识该执行单元的定位信息，如线程号，线程块号等，需要通过特定的指令来读取这些寄存器，常见的特殊寄存器如下，其中SR_TID表示cuda thread block内的线程id即cuda编程中的threadIdx，SR_CTAID表示线程块id即cuda编程中的blockIdx，还有其他的获取硬件SM id、时间信息等的特殊寄存器，如下

SR_TID.X, SR_TID.Y, SR_TID.Z,
SR_CTAID.X, SR_CTAID.Y, SR_CTAID.Z,
SR_VIRTUALSMID, SR_LANEID, SR_LEMASK, SR_LTMASK, SR_GEMASK,
SR_CLOCKLO, SR_CLOCKHI
SR_GLOBALTIMERLO, SR_GLOBALTIMERHI
SRZ
SR_PM0-7
SR_SMEMSZ

nvidia官方也给出了对应的文档。

predicate寄存器

用来做GPU分支预测的，这个跟CPU的分支预测不同，这个用于控制线程束warp中线程的执行流程。

P0, P1, P2, P3, P4, P5, P6, P7(PT)

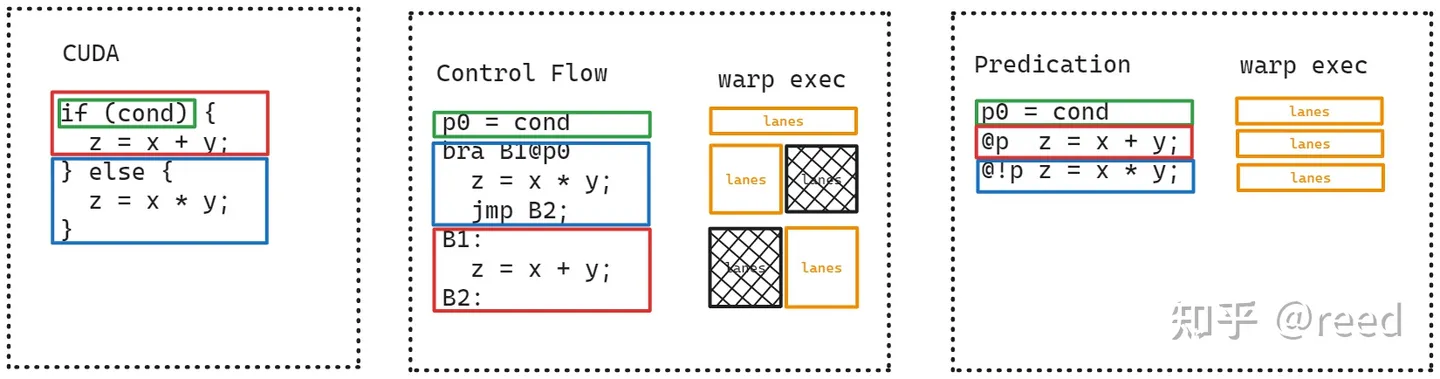
如图所示，对于CUDA指令，相较于没有使用predicate寄存器的中间版本（存在一个分支延迟），后者显然性能更高。

具体地，Predicate寄存器主要有两个作用：一个是作为指令的执行条件放在指令的开始，如@P6 FADD R5 R5 R28; 和@!P1 FADD R11 R11 R17; 用以指示该条指令为条件指令，只有当@后的predicat运算结果为True时才会执行，反之为False时，该指令不产生执行副作用；二是predicate可以作为操作数参与特定指令的运算，如FMNMX R9 RZ R6 !PT;。Predicate寄存器为每个线程私有，每个线程最多可使用8个，在SASS表示中名称以P为前缀，表示为P0-P7，其中P0-P6为常规的读写Predicate寄存，P7为常真寄存器，即它始终为True，SASS中标示为PT（Predicate True）：

Uniform寄存器

上面的几个寄存器都是线程私有的寄存器，有些场景一个warp内的所有lane会执行完全相同的逻辑或者做reduce等功能（CUDA对应__reduce_sync类函数），NV提供了Uniform寄存器、Uniform Predicate和相应的指令来完成Warp Level的公共计算。使用Uniform寄存器可以减少对私有寄存器的使用量，继而可以减少warp对通用寄存器的使用，使得SM上有机会运行更多的warp提升并发度，同时由于Warp Level不需要向量化的执行单元，也能减少整体芯片功耗。在SASS层面，Uniform寄存器以UR作为前缀，单个warp最多可用64个，Uniform Predicate以UP作为前缀，单个warp最多可用7个，和通用寄存器、Predicate类似，最后一个寄存器UR63为常零寄存器，SASS中表示为URZ（Uniform Register ZERO），类似地，也有常真Uniform Predicate UPT（Uniform Predicate True）。

UR0, UR1, UR2, UR3, ..., UR60, UR61, UR62, UR63（URZ）
UP0, UP1, UP2, UP3, UP4, UP5, UP6, UP7(UPT)

Load 和 Cache

在最早接触CUDA编程的时候我们就知道了CUDA计算的整个架构，以ampere架构为例

具体的一些架构方面的就不必多说了，这里的重点在于一些指令集的学习和了解：

数据load指令

数据加载相关的指令整体如下：

LD, LDG, LDS, LDSM, LDL

其中LD指令（LoaD），是通用的（编译器在编译时无法推导地址空间类型的数据加载），如果编译时可以明确的知晓地址空间类型则使用有类型的加载指令LDG（LoaD Global memory），LDS（LoaD Shared memory），LDSM（LoaD Shared Matrix），LDL（LoaD Local memory）等，具体地：

全局内存到寄存器：

LDG.类型.向量.Cache控制.L2预取

加载全局内存地址中的数据到寄存器，可以配置加载时的数据宽度，如8bit数据，16bit数据，128bit数据等。同时可以配置各层级的Cache的bypass等情况，也可以配置是否对数据向L2中预取。单就指令而言向量化的数据加载（或叫大字长加载）如LDG.128是NVidia GPU支持的最大的加载指令，一条指令可以加载128bit数据，对于同等规模的数据使用更宽的加载指令可以减少warp对指令的调度次数，减少调度开销，减少MIO queue的事务数，避免由于queue满而造成阻塞。除了单指令位宽，更高效的数据加载还需要考虑合并访存。

全局内存到共享内存：

LDGSTS, LDGDEPBAR, DEPBAR.LE SB0, 0x1

异步读取数据全局内存并将结果存储到共享内存LDGSTS（LoaD Global memory STore Shared memory），可以实现不经过寄存器的全局内存到共享内存数据搬运，可以减少寄存器的使用和依赖，在矩阵计算中，尤其Multi Stage的矩阵计算中有重要作用，可以参考cute之GEMM流水线的异步拷贝章节。同时该指令要结合Barrier设置和等待指令（LDGDEPBAR，DEPBAR）协同使用。另外该指令在加载数据时可以指定是否在L1进行Cache，和对L2进行数据预取。

共享内存到寄存器：

LDS.类型.向量化，LDSM.块.转置

LDS的modifer可以设置数据位宽信息，和LDG类似高位宽的指令可以减少warp指令的调度数减少MIO queue中的事务数目，防止queue满引起的阻塞。LDSM为warp级协作指令，完成共享内存到寄存器的数据加载，进而将这些寄存器feed给Tensor Core指令完成矩阵计算，更细节的介绍可以参考cute之Copy抽象和ldmatrix指令优势介绍。

局部数组和寄存器溢出：

LDL

目前认为有三种情况可以引入Local Memory：1. 当线程计算需要局部数组，并且数组的下标不能被编译时计算时；2. 单线程的寄存器使用数目超过255；3. 访问kernel数组常量时使用了不能被编译时确定的索引。Local Memory是CUDA编程中的一个概念，它的物理实体是全局内存中的一段。当上面情况发生时，每一个线程都会被分配一段全局内存来作为数据空间，由于数据需要对全局内存进行读写，一般而言对于线程数比较多的场景，其开销很大，除非万不得已，应该尽量能避免Local Memory的使用。

常量Cache：

提供了一个广播语义，即warp内的所有线程都访问同一个数据时，它的访问速度和寄存器一样快，所以其可以被直接编码在指令操作数中。另外我们可以实现device端的可编程常量（__constant__ __device__ int a;）。当warp内的线程访问同一个constant位置时，其是确定的latency的。

寄存器reuse和prefetch：

除了以上常规的存储机构和Cache，在计算单元流水线中，已经加载进计算单元流水线的数据也可以复用，其体现为寄存器的reuse，我们可以把它当做寄存器cache，它可以减少寄存器带宽压力一定程度上降低功耗，如

R1.reuse

除了前面提到的Load指令可以做伴随的数据预取，SASS还提供了显式设置L1/2 Cache的预取指令，如（CCTL = Cache ConTroL）

CCTL.E.PF2

浮点数

浮点数的表示自然不必多说，这里还是着重说明GPU中浮点数相关的内容。

不同的设备有着不同浮点数的支持，比如Ampere架构支持：float32, float16(half), bfloat16, tfloat32, double. hopper添加了float8类型并根据指数和尾数数量分为E5M2和E3M4类型，blackwell添加了fp4类型，具体如下图：

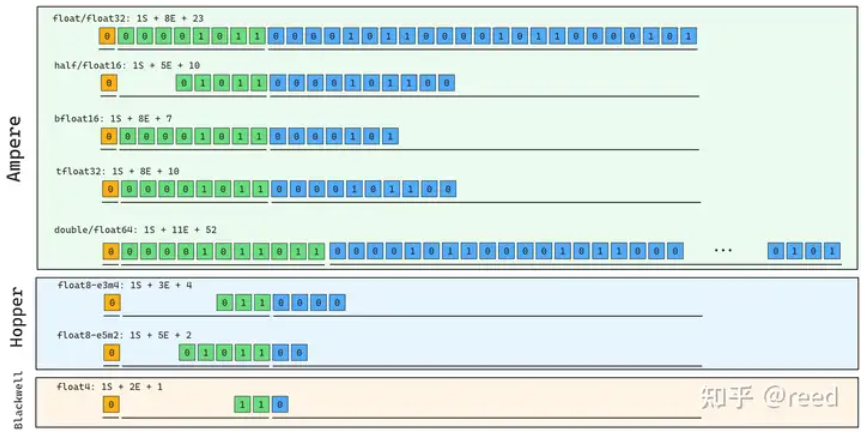
浮点数的圆整则是比较简单的，可以分为向最近圆整，向零圆整，向正无穷圆整（up）和向负无穷圆整（down），这个倒是不必多说。

浮点数特殊值

浮点数的指数全0和全1是被保留的，全1表示为NaN，对于CUDA而言不算异常，且由于该数值的传递性，因此如果中间或者最后出现了NaN，那就说明中间出现了异常。（此外NaN * 0不为0，这种情况通常是由于没有好好做初始化导致的）

GPU浮点数操作

乘、加操作

很多很多：

FADD R0 R1 R2;     // R0 = R1 + R2  with round to NEAREST
FADD.RZ R0 R1 R2;  // R0 = R1 + R2 with round to ZERO
FADD.RP R0 R1 R2;  // R0 = R1 + R2 with round to POSITIVE(+Infinity)
FADD.RM R0 R1 R2;  // R0 = R1 + R2 with round to MINUS(-Infinity)
FMUL R0 R1 R2;     // R0 = R1 * R2 with round to NEAREST
FMUL.RZ R0 R1 R2;  // R0 = R1 * R2 with round to ZERO
FMUL.RP R0 R1 R2;  // R0 = R1 * R2 with round to POSITIVE(+Infinity)
FMUL.RM R0 R1 R2;  // R0 = R1 * R2 with round to MINUS(-Infinity)

DADD R0 R2 R4;     // R0.64 = R2.64 + R4.64 with round to NEAREST
DADD.RZ R0 R2 R4;  // R0.64 = R2.64 + R4.64 with round to ZERO
DADD.RP R0 R2 R4;  // R0.64 = R2.64 + R4.64 with round to POSITIVE(+Infinity)
DADD.RM R0 R2 R4;  // R0.64 = R2.64 + R4.64 with round to MINUS(-Infinity)
DMUL R0 R2 R4;     // R0.64 = R2.64 * R4.64 with round to NEAREST
DMUL.RZ R0 R2 R4;  // R0.64 = R2.64 * R4.64 with round to ZERO
DMUL.RP R0 R2 R4;  // R0.64 = R2.64 * R4.64 with round to POSITIVE(+Infinity)
DMUL.RM R0 R2 R4;  // R0.64 = R2.64 * R4.64 with round to MINUS(-Infinity)

这里就不再赘述了，整体来说看注释就可以。

乘加操作

这个相加于前面的操作而言性能会高一点，前面的操作实际上是两条指令，但是中间会有吞吐下降以及精度损失（乘加操作中间是无限精度的而不需要圆整）：

FFMA R0, R1, R2, R3;  // R0 = R1 * R2 + R3 with round to NEAREST
FFMA.RZ R0, R1, R2, R3;  // R0 = R1 * R2 + R3 with round to ZERO
FFMA RP R0, R1, R2, R3;  // R0 = R1 * R2 + R3 with round to POSITIVE
FFMA.RM R0, R1, R2, R3;  // R0 = R1 * R2 + R3 with round to MINUS

DFMA R0, R2, R4, R6;  // R0 = R2 * R4 + R6 with round to NEAREST
DFMA.RZ R0, R2, R4, R6;  // R0 = R2 * R4 + R6 with round to ZERO
DFMA RP R0, R2, R4, R6;  // R0 = R2 * R4 + R6 with round to POSITIVE
DFMA.RM R0, R2, R4, R6;  // R0 = R2 * R4 + R6 with round to MINUS

随路取负

CUDA指令集不包含减法，但是都可以通过取负直接实现：

FADD R0 R1 -R2;     // R0 = R1 - R2  with round to NEAREST
FADD.RZ R0 R1 -R2;  // R0 = R1 - R2 with round to ZERO
FADD.RP R0 R1 -R2;  // R0 = R1 - R2 with round to POSITIVE(+Infinity)
FADD.RM R0 R1 -R2;  // R0 = R1 - R2 with round to MINUS(-Infinity)

可以应用于前面的ADD、MUL、FMA操作，

低精度浮点数操作

前面提到了CUDA支持低精度的浮点数操作，但是由于寄存器位数就是32位的，所以实际操作是进行一个packed进行。即使是单个half也是使用针对pakced的指令。

对于half2同样提供了乘法、加法和乘加操作，但是这些指令的圆整就只有圆整这一种方式，并提供了一些modifier进行截断操作（SAT截断到[0,1]，ReLU）取负操作是随路取负。

而对于bfloat162，则没有加法和乘法指令，只提供了乘加指令，因此进行加法乘法都是通过这一条指令实现的，同样有随路取负但是modifier只有ReLU，相较于half算是进一步阉割了（bfloat全程brain float，是由google提出的浮点数类型，只有Ampere架构之后才支持，且精度低，范围大（指数8位尾数7位））：

HADD2 R7, R0, R7;
HMUL2 R7, R0, R7;
HADD2.SAT R7, R0, R7;
HMUL2.SAT R7, R0, R7;

HFMA2.MMA R7, R0, R7, R6;
HFMA2.MMA.SAT R7, R0, R7, R6;
HFMA2.MMA.RELU R7, R0, R7, R6;
HADD2 R7, |R2|, -RZ.H0_H0;
HADD2 R7, -R2, -RZ.H0_H0;
HADD2 R7, R0, -R7;

HFMA2.BF16_V2 R7, -RZ.H0_H0, RZ.H0_H0, |R2|;
HFMA2.BF16_V2 R7, R0, 1, 1, R7;
HFMA2.BF16_V2 R7, R0, R7, R6;
HFMA2.BF16_V2.RELU R7, R0, R7, R6; 
HFMA2.BF16_V2 R7, R0, R7, -RZ.H0_H0;
HFMA2.BF16_V2 R7, -RZ.H0_H0, RZ.H0_H0, -R2;
HFMA2.BF16_V2 R7, R7, -1, -1, R0;

类型转换

考虑到寄存器的位数和不同数据类型的别扭程度，类型转换也不是件容易的事情：

转换成->	float64	float32	half	bfloat16
float64	/	F2F.F32.F64	F2F.F16.F64	Multi-Instr
float32	F2F.F64.F32	/	F2FP.PACK_AB	F2FP.BF16.PACK_AB
half	Multi-Instr	HADD2.F32	/	NA
bfloat16	Multi-Instr	PRMT	NA	/

其中Multi-Instr表示需要多条指令实现。

超越函数

超越函数指的是一些特殊的浮点运算操作比如sqrt、log、rcp、三角函数等，这些操作是在特殊计算单元实现的，底层的实现并不是进行真正的对应计算，而是使用二次函数进行逼近实现的，对不同的区段采用不同的a、b、c来实现相对高精度的结果（这样看来就是个查表过程）：

MUFU.EX2 R7, R6 ;
MUFU.SIN R7, R7 ;
MUFU.COS R7, R7 ;
MUFU.LG2 R7, R0 ;
MUFU.RCP R7, R6 ;
MUFU.RSQ R5, R2 ;
MUFU.SQRT R7, R13 ;
MUFU.TANH R11, R4 ;

先对来说精度偏低，编译器会对其进行修正得到更高精度结果，如果不需要高精度则可以加双下划线表示__从而提高性能。

除法

除法一直是一个非常尴尬的问题，现在的计算单元对于除法的支持依旧不是很好，所以在绝大多数情况下还是使用乘法会更好一点，对于CUDA指令集，则是通过特殊函数的RCP倒数+ADD、MUL、FMA泰勒展开进行高阶修正得到的，比如一个normal数的除法5阶泰勒修正如下：

MUFU.RCP R8, R5 ;          /* 0x0000000500087308 */ /* 0x000e220000001000 */
FADD.FTZ R10, -R5, -RZ ;                            /* 0x800000ff050a7221 */
FFMA R3, R8, R10, 1 ;                               /* 0x3f80000008037423 */
FFMA R12, R8, R3, R8 ;                              /* 0x00000003080c7223 */
FFMA R3, R7, R12, RZ ;                              /* 0x0000000c07037223 */
FFMA R8, R10, R3, R7 ;                              /* 0x000000030a087223 */
FFMA R11, R12, R8, R3 ;                             /* 0x000000080c0b7223 */
FFMA R7, R10, R11, R7 ;                             /* 0x0000000b0a077223 */
FFMA R3, R12, R7, R11 ;                             /* 0x000000070c037223 */

除此之外

除此之外还有一些控制流、比较大小、是否Normal、取整等操作：

FSETP
FMNMX
FCHK
FRND  FRND.CEIL  FRND.F16.FLOOR  FRND.F64.FLOOR  FRND.FLOOR

整数操作

本来浮点数算是相当重要的成分，但是现在各种量化的操作让整数操作也非常重要了，具体的包含统计、排序、计数、地址计算、索引、加密验证、量化等等等等，虽然应用比较复杂但是脱离不了简单的数据操作。

符号	类型	字节数	最大值	最小值
有符号	int8_t	1	-128	127
有符号	int16_t	2	-32768	32767
有符号	int32_t	4	-2147483648	2147483647
有符号	int64_t	8	-9223372036854775808	9223372036854775807
无符号	uint8_t	1	0	255
无符号	uint16_t	2	0	65535
无符号	uint32_t	4	0	4294967295
无符号	uint64_t	8	0	18446744073709551615

整数有非常多的数据类型，但是实际上没什么影响，用的都是32bit的加法单元，对于大于32bit的使用拼接（分成两个或者多个部分相加），对于小于32bit的补0操作即可。

由于整数只有32bit的计算指令，因此使用低bit整数计算并不会提高性能，只能减少空间存储。

整数加法

不必多说：

// 8bit, 16bit, 32bit
IADD3 R7, R0, R7, RZ ; // R7 = R0 + R7 + RZ

// substraction
IADD3 R7, R0, -R7, RZ ;

// 64bit R6-7 = R4-5 + R6-7
IADD3 R6, P0, R4, R6, RZ ;  // (R6, P0) = R4 + R6 + R0; P0 indicate carry
IADD3.X R7, R5, R7, RZ, P0, !PT ; // R7 = R5 + R7 + RZ + P0;

使用IADD3实现d=a+b+c，对于64bit稍微有点区别，先计算低32bit的情况之后把多出来的进位交给高位计算。注意，其中有一个寄存器虽然不起眼但是很厉害，就是P0寄存器，其就是前面说到的prodication register，用于辅助判断下面是否需要进行进位加

整数乘法

指令集没有乘法，只有乘加形式，其余的特殊功能通过modifier形式提供：

IMAD
IMAD.HI
IMAD.HI.U32
IMAD.IADD
IMAD.IADD.U32
IMAD.MOV 
IMAD.MOV.U32
IMAD.SHL
IMAD.SHL.U32
IMAD.U32
IMAD.U32.X
IMAD.WIDE
IMAD.WIDE.U32
IMAD.WIDE.U32.X
IMAD.X

比如计算高32bit的HI、ADD(b=1), SHL(b=2,4,…), MOV(a=0, b=0)，整体来说非常有用

整数位移

SHF.L.U32
SHF.L.U32.HI
SHF.L.U64.HI
SHF.L.W.U32
SHF.R.S32.HI
SHF.R.S64
SHF.R.U32.HI
SHF.R.U64

用LR指定左移右移，U32U64表示对应数据类型逻辑位移，S32S64表示对应数据类型算术位移

除法和取余

没有除法操作，需要先倒数再用浮点计算最后转换为整数。但是如果除数编译为常量时，编译器会使用数学变换将除法变成位移和乘法指令

整数转浮点数

默认转化为f32

I2F
I2F.F16
I2F.F64
I2F.F64.S64
I2F.F64.U32
I2F.F64.U64
I2F.RP
I2F.S16
I2F.S64
I2F.S8
I2F.U16
I2F.U32
I2F.U32.RP
I2F.U64
I2F.U64.RP

packed

除了大数方便用于操作，也有对应的pack操作：

I2IP.S8.S32.SAT

Integer2Integer pack

整数绝对值

有这个指令：

IABS

整数点积

出现在深度学习场景用于低精度整数点积运算：

IDP.2A.LO.U16.U8
IDP.4A.S8.S8

整数最大最小

IMNMX R7, R0, R7, !PT ; // when PT return R7 = min(R0, R7), when !PT R7 = max(R0, R7)
IMNMX.U32

为了避免分支同时使用了大数据和小数据，对于64bit数据需要使用ISETP实现

整数比较

前面刚说完ISETP,现在场景就出来了，通过组合可以实现复杂的操作：

ISETP.EQ.AND      ISETP.EQ.U32.OR  ISETP.GE.OR.EX       ISETP.GT.AND.EX      ISETP.GT.U32.OR   ISETP.LT.AND      ISETP.LT.U32.AND.EX  ISETP.NE.OR.EX
ISETP.EQ.AND.EX   ISETP.EQ.XOR     ISETP.GE.U32.AND     ISETP.GT.OR          ISETP.LE.AND      ISETP.LT.AND.EX   ISETP.LT.U32.OR      ISETP.NE.U32.AND
ISETP.EQ.OR       ISETP.GE.AND     ISETP.GE.U32.AND.EX  ISETP.GT.OR.EX       ISETP.LE.OR       ISETP.LT.OR       ISETP.NE.AND         ISETP.NE.U32.AND.EX
ISETP.EQ.OR.EX    ISETP.GE.AND.EX  ISETP.GE.U32.OR      ISETP.GT.U32.AND     ISETP.LE.U32.AND  ISETP.LT.OR.EX    ISETP.NE.AND.EX
ISETP.EQ.U32.AND  ISETP.GE.OR      ISETP.GT.AND         ISETP.GT.U32.AND.EX  ISETP.LE.U32.OR   ISETP.LT.U32.AND  ISETP.NE.OR

Tensor Core整数指令

另外NVidia GPU通过Tensor Core提供了算力更高的整数类型矩阵乘法指令，我们会在后面章节更详细的介绍：

IMMA.16816.S8.S8
IMMA.16832.S8.S8.SAT
IMMA.8816.S8.S8.SAT

比特和逻辑操作

对于计算机的寄存器而言，其并不理解所存储的数据的类型而只是简单的进行数据的存储，对于同样的数据，根据不同的类型就可以被解释成不同的表示，也因此可以进行很多操作。

POPC

POPC(POPulation Count，真的命名鬼才)用于计算32bit寄存器中1的个数，对于64bit同样可以执行该操作，只不过需要分成高低位进行：

POPC R7, R2;

FLO

FLO(First Leading One)从高位到低位第一个1的位置，如果输入全为0则0xFFFFFFFF,如果全为1则：31

FLO.U32 R0, R2;

只提供32bit的计算操作，对于64bit则需要多条指令组合，此外还可以根据正负分析,正数则找从高位开始找第一个1，负数则从最高位开始找第一个0，同时该指令还提供了SH modifier，该modifier可以返回将前面的index调整到符号位置所需要的左移量：

FLO R7, R2 ; // signed find leading one
FLO.U32.SH R7, R2 ;
FLO.SH R7, R2 ;

BREV

BREV(Bit REVerse)bit逆序，实现32bit数据高低位交换

BREV R7, R2 ;

SGXT

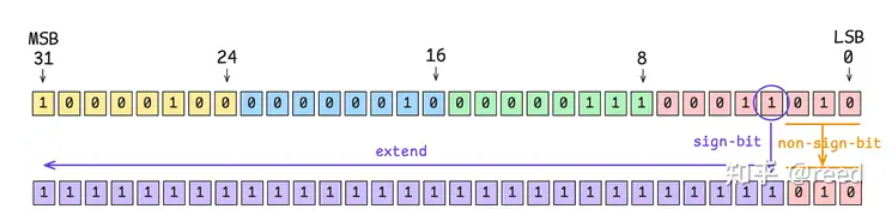
SGXT(SiGn eXTend)指令，实现特定bit位数据的符号位拓展

SGXT R7, R0, R7 ;  // nbit = R7

BMSK

从start位置填充mask个1

BMASK R2 R0 R1; // start: R0, mask: R1;
BMSK R5, R5, 0x3 ;

PRMT

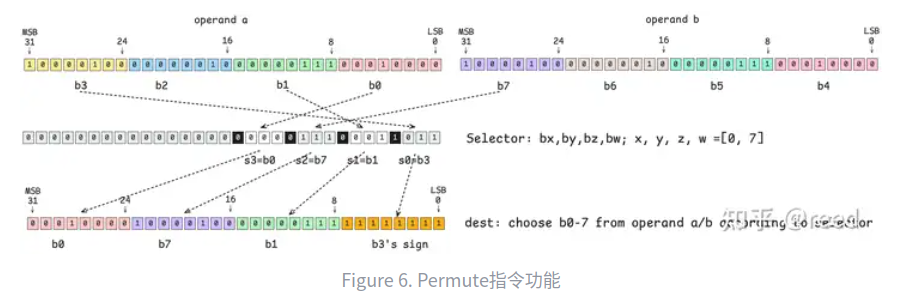
PRMT(ReRMuTe)以8bit为单位进行重新排序，算是位操作里面比较重要的一个指令了。

// RRMT Rd Ra Rb Rsel;
PRMT R7 R4 R5 R6;

如图6所示，Ra每8bit构成一个最小的byte单位，从低到高被编号为b0, b1, b2, b3; Rb每8bit表示一个最小单位，从低比特位向高位依次被标记为b4, b5, b6, b7。Rsel寄存器用来指定b0-7的编号，即从b0-b7中选择4个字节（可以重复）重新输出到一个32bit的寄存器中。Rsel需要选择4个编号来完成32bit的输出，每个字段占用4bit，其中每个字段的低3bit表示operand a/b中选取的byte的编号，4bit中的高bit表示该选择的编号位置是原值复制还是重复符号位（0表示原值复制，1表示填充符号位）。也就说结果中的高8bit（24-31bit）是由Rsel中的12-15bit决定的（s3=b0），其中12-14bit用来决策选择operand a/b中的第几个byte，如图所示，其bx=0b000=0表示选择operand a/b中的b0段，且最高位（15bit）位0表示原值复制，这样operand a b0位置的数据则复制到输出位置（24-31bit），类似地，输出位置的16-23bit由Rsel的第二个4bit（s2=0b111=7）控制，表示选择b7，即operand b中的b7所对应的8bit数据，同时该控制Rsel 4bit中的最高位为0表示复制原值，输出位置的8-15bit来自operand a的b1位置，输出位置0-7bit由Rsel的s0（s0=0b1011）控制，其中低3bit表示来自于b的序号，为3，高1bit表示复制符号位，则其综合表示复制b3的符号位，且将该符号位填充输出的8bit，结果上表现为Rd的0-7bit为全1。

LOP3

LOP3 （ Logical OPeration on 3 inputs）

对三个数据进行位操作，而具体的操作根据查找表(LUT, Look Up Table)进行：

LOP3.LUT R7, R0, R7, R6, 0xf, !PT ;

其中R0, R7, R6为操作数，R7为目的数，0xf则是查表