Diffusion

在Diffusion之前的生成模型是GAN，但是显然性能不行，所以就开始转向Diffusion了。最早期来源于: DDPM: Denoising Diffusion Probabilistic Models

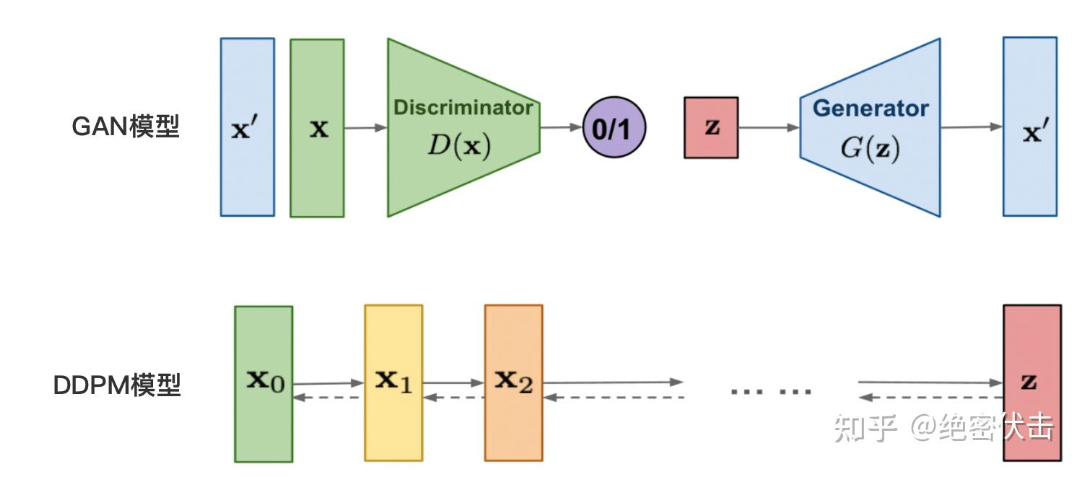
DDPM原理整体来说还是很容易理解的，DDPM分成两个过程，前向过程和反向过程。（注意，下图是一个反向过程）

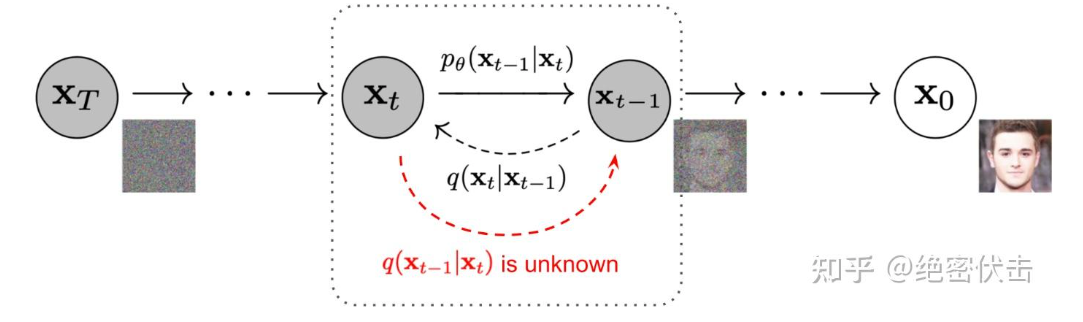
前向传播过程是一个不断向图片中加入噪声的过程：

$$X_t = \sqrt{\alpha_t}X_{t-1} + \sqrt{1-\alpha_t}\epsilon_{t-1}$$

其中a是一个超参数，e是加入的高斯噪声，

反向过程就是一个去噪的过程，

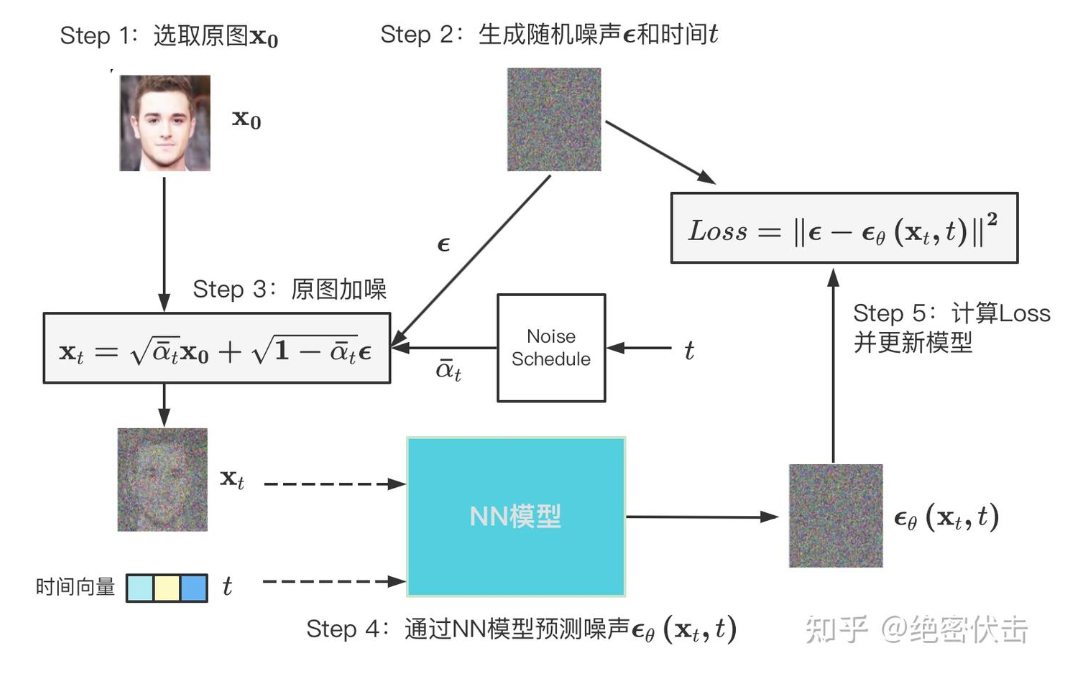
整体的训练过程：

Stable Diffusion

上述的Diffusion只能根据timestep来改变生成的效果，但是在图像生成领域其实更倾向于条件生成，也就是接下来的Stable Diffusion。

其实也不复杂，文本输入时候进行文本的embedding操作，之后和噪声一起加入到diffusion中训练即可。

DiT

基于Diffusion + Transformer

基本原理不变，但是相较于U-Net，符合Scaling law，因此可以随着参数量提升提高生成效果。

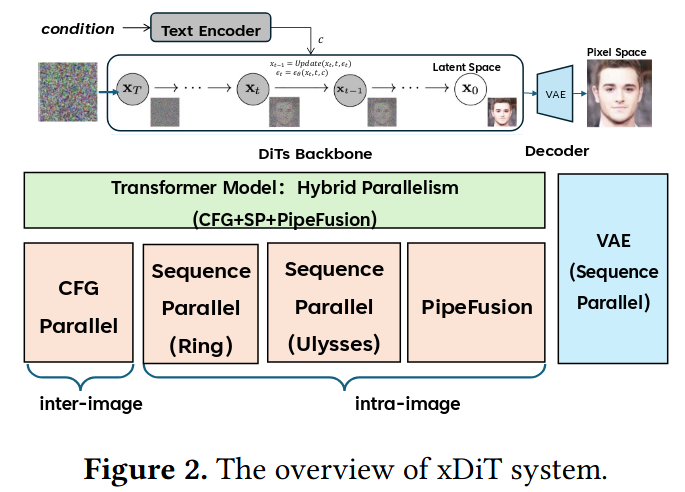
xDiT

具体可以参考这篇blog：https://blog.csdn.net/daydayup858/article/details/144209090

xDiT要面临的问题比较多

• 与LLM推理不一样，DiT的推理是计算密集的
• 图像生成的模型参数量可以非常大
• 不同的模型架构存在较大的差异

From another View of Diffusion

生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼

首先，科学空间苏神的讲解非常详细和简单。

但是还有一些需要注意的细节，由于Diffusion的采样器诸多，现在较好的采样器层出不穷，其中不同的迭代次数也会存在不同，在最早期的DDPM中需要使用1000次的迭代来达到较好的效果，其中的一个设计细节就是噪声强度是随着迭代次数单调递减的函数

相较于VAE，为了突破单步生成的限制，DDPM将编码过程和生成过程分解为T步：

编码:x=x0→x1→x2→⋯→xT−1→xT=z生成:z=xT→xT−1→xT−2→⋯→x1→x0=x(2)(2)编码:x=x0→x1→x2→⋯→xT−1→xT=z生成:z=xT→xT−1→xT−2→⋯→x1→x0=x

这样一来，每一个p(xt|xt−1)p(xt|xt−1)和q(xt−1|xt)q(xt−1|xt)仅仅负责建模一个微小变化，它们依然建模为正态分布。可能读着就想问了：那既然同样是正态分布，为什么分解为多步会比单步要好？这是因为对于微小变化来说，可以用正态分布足够近似地建模，类似于曲线在小范围内可以用直线近似，多步分解就有点像用分段线性函数拟合复杂曲线，因此理论上可以突破传统单步VAE的拟合能力限制。