性感100题
着重解决一下hot100题，下面的实现都以python进行。
哈希表
哈希表算是最常用的数据结构之一，对于python而言，哈希表的选择有很多，最简单的是dict()，初次之外还有Collections中的OrderedDict, Counter等等，当然，这些都是会用到的，只是具体的情况不同。
首先对于dict()其就是一个简单的字典，算是最小的一个hash类别，其在简单场景下可以轻松的使用，并可以使用字典推导式来简洁写法。OrderedDict使用场景较少，需要用到的时候再说。Counter算是对可迭代数据的一个处理，对可迭代的数据进行一个计数统计。接下来就是三道哈希表的
1. 两数之和
- 从一个无序数组中找到两个数字使得和等于target
49. 字母异位词分组
- 将一个列表中的不同字符串，根据是否包含完全一样的字符串分到不同的数组中
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
128. 最长连续序列
- 找到最长的连续的序列长度
输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
双指针
283. 移动零
- 原地把0放到数组末尾
11. 盛最多水的容器
- 计算两个竖线中间容纳水的最大值
15. 三数之和
- 找到三个数字的和为0
42. 接雨水
- 接雨水
滑动窗口
需要单调性
3. 无重复字符的最长子串
- 找到没有重复字符的子串
438. 找到字符串中所有字母异位词
- 前面异位词的简单升级版
子串
560. 和为 K 的子数组
- 找到和为k的连续数组
239. 滑动窗口最大值
- 返回序列中窗口的最大值列表
76. 最小覆盖子串
- 找到覆盖子串的最小长度子串
普通数组
53. 最大子数组和
- 找到最大的连续的子数组的和
56. 合并区间
- 合并区间
189. 轮转数组
- 数组右移k位
- 给你一个数组，对每个元素计算$prod(nums)/nums[i]$ 但是不能除法
41. 缺失的第一个正数
- 找到一个数组里缺失的第一个正数
矩阵
73. 矩阵置零
- 将0所在的行列置0
54. 螺旋矩阵
- 螺旋输出数组
48. 旋转图像
- 旋转一下矩阵90度
240. 搜索二维矩阵 II
- 行列均是升序，高效查找到某个target值
链表
160. 相交链表
- 两个列表找到相交的节点
206. 反转链表
- 反转链表
234. 回文链表
- 判断链表是不是回文的
141. 环形链表
- 看看链表是否有环
142. 环形链表 II
- 找到环的位置
21. 合并两个有序链表
- 合并有序链表
2. 两数相加
- 把链表表示的数值求和
19. 删除链表的倒数第 N 个结点
- 删除链表的倒数第 N 个结点
24. 两两交换链表中的节点
- 两两交换链表中的节点
25. K 个一组翻转链表
- 以k个单位为一组反转链表
树
94. 二叉树的中序遍历
- 二叉树中序遍历
104. 二叉树的最大深度
- 二叉树的最大深度
226. 翻转二叉树
- 翻转兄弟节点
101. 对称二叉树
- 判断是否关于root结点轴对称
543. 二叉树的直径
- 找到最长的路径
102. 二叉树的层序遍历
- 层序遍历二叉树
108. 将有序数组转换为二叉搜索树
- 将有序数组转换为二叉搜索树
98. 验证二叉搜索树
- 判断是不是一个二叉搜索树
230. 二叉搜索树中第 K 小的元素
- 找二叉搜索树中第k小的元素
199. 二叉树的右视图
- 想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
114. 二叉树展开为链表
- 将一个二叉树前序遍历展开成链表
105. 从前序与中序遍历序列构造二叉树
- 根据先序和中序遍历构造二叉树
437. 路径总和 III
- 求二叉树里节点值之和等于
sum的路径数量
236. 二叉树的最近公共祖先
- 给两个节点找祖先
图论
200. 岛屿数量
- 计算岛屿的数量
994. 腐烂的橘子
- 腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂
207. 课程表
- 单项依赖的课程能否学完
回溯
回溯最经典的题目就是N皇后问题了，对于回溯问题之前并没有详细的刷过，因此这次得重新理解一下了。首先，对于python是有原生的permute函数的：
from itertools import permutations
return list(permutations(nums))
但是这一点只是应用，关键是如何更好的理解这个过程。从名字就可以看出来，这类题目的核心就是构建一棵树并逐渐添加节点，最后枚举叶子节点即可，因此通常来说并不是特别复杂吗？显然不是，对于简单的题目可以直接permute，但是对于复杂的场景，往往还需要去重等操作，也就是接下来要学习的了。
46. 全排列
- 返回数组的全排列列表
78. 子集
- 返回数组所有不相同的子集
17. 电话号码的字母组合
- 返回每个数字表示的字符所能组成的单词可能
39. 组合总和
- 返回能够得到某个数的数字所有数字集合（找零钱）
22. 括号生成
- 给定n生成符合条件的n个括号的所有可能字符串
79. 单词搜索
- 棋盘中是否包含某个单词可以通过dfs找到
131. 分割回文串
- 将字符串分割成回文串的集合。
51. N 皇后
- 皇后摆放且不能对角线上下左右存在
二分查找
在印象中二分其实是比较常见但是整体来说比较模板化的题目，所以先记下一个模板：
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return left
35. 搜索插入位置
- 如果查到数字就返回对应的位置，否则返回应该插入的位置
74. 搜索二维矩阵
- 二维数组从左往右从上往下递增，查找
34. 在排序数组中查找元素的第一个和最后一个位置
- 找target第一个和最后一个位置
33. 搜索旋转排序数组
- 数组根据某个值旋转之后查找到对应的元素
153. 寻找旋转排序数组中的最小值
- 找旋转排序数组最小值
4. 寻找两个正序数组的中位数（not done）
- 找两个升序数组的中位数
栈
20. 有效的括号
- 判断字符串是否是正确的括号
155. 最小栈
- 数据结构题目实现一个最小栈
贪心算法
121. 买卖股票的最佳时机
- 一个时间点买一个时间点卖求最大收益
55. 跳跃游戏
- 能否跳到最后的位置
45. 跳跃游戏 II
- 比刚才稍微复杂，判断跳到最后一格最少需要多少次跳
763. 划分字母区间
- 划分包含相同字母的区间
动态规划
70. 爬楼梯
- 每次爬1、2层，到n层的方法数量
技巧
- 找哪个数字只出现过一次
169. 多数元素
- 数量超过【n/2】的元素
75. 颜色分类
- 0,1,2排序
题解-哈希表
1. 两数之和
- 思路1: 使用排序之后使用双指针扫描即可，复杂度为$O(nlogn)$算是比较高的复杂度了：
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
nums=[[j, i] for i,j in enumerate(nums)]
nums=sorted(nums)
print(nums)
ln=len(nums)
l, r = 0, ln-1
while l < r:
if nums[l][0]+nums[r][0] > target:
r -=1
elif nums[l][0]+nums[r][0]<target:
l+=1
else:
return [nums[l][1],nums[r][1]]
- 思路2:既然这一部分是hash的相关内容，那么自然也可以使用hash来解决上述问题，构建一个hash表，从中查询元素，直到两者和等于target
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashtable = dict()
for i, num in enumerate(nums):
if target - num in hashtable:
return [hashtable[target - num], i]
hashtable[nums[i]] = i
return []
相较于官方的题解，自己的思路果然还是复杂了一点。官解在进行遍历时就顺便查找其中的值，使得整体代码更简洁了。
49. 字母异位词分组
- 思路：对字符重排序之后作为字典的键，并存储每个repo的index即可 ，整体来说也不复杂：
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
res = []
d = dict()
ld = 0
for i in strs: # 注意str sorted是对字符进行排序，还需要试用一下join
si = "".join(sorted(i))
if d.get(si, None) is None:
d[si] = ld
res.append([])
res[ld].append(i)
ld += 1
else:
nd = d[si]
res[nd].append(i)
return res
唯一要注意的就是其中的sorted对于字符串实际上是先list后sorted。
128. 最长连续序列
- 思路：利用字典记录一下，之后每次查询+i和-i个元素，并想办法把这些查过的元素删除防止多次计算。这里有两个很坑的地方，首先，对于python，set的查询速度同样为
O(1)，因此可以考虑使用set直接做in操作查询。其次，使用字典删除元素的复杂度会偏高，导致超时，因此合理的做法是利用set做查询，之后尝试标记防止多次查询。实际的实现更加细节：
#相对来说最完美的
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if not nums:
return 0
num_set = set(nums) # 转换为集合，去重
max_length = 0
for num in num_set:
# 只有当 num-1 不存在时，才开始计算序列
# 这确保了每个序列只被计算一次
if num - 1 not in num_set:
current_num = num
current_length = 1
# 向后查找连续序列
while current_num + 1 in num_set:
current_num += 1
current_length += 1
max_length = max(max_length, current_length)
return max_length
核心在于num-1不存在时的序列计算。另一种比较好想但是不优雅的方式如下：
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
d = set(nums)
max_len = 0
while d:
# print(d)
nc = d.pop()
cur_len = 1
# forward
for i in range(1, 100_000):
if nc + i not in d:
break
else:
cur_len += 1
d.remove(nc+i)
# backward
for i in range(1, 100_000):
if nc - i not in d:
break
else:
cur_len += 1
d.remove(nc-i)
max_len = max(max_len, cur_len)
return max_len
每次pop出来一个元素之后查询，查到一个就删除一个，当然也可以使用额外数组来保存。
题解-双指针
283. 移动零
- 思路：其实如果不限制原地和额外空间的话思路很多，什么栈、队列、排序基本上都可以。但是题目说了原地置换和$O(1)$空间，所以就只能用双指针了，代码如下：
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
left = right = 0
while right < n:
if nums[right] != 0:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right += 1
11. 盛最多水的容器
- 思路：正常来求解的话肯定是枚举所有的列可能性，这种情况下复杂度直接$O(n^2)$所以肯定不能采取，所以核心在于如何消除多余的状态。其实不难想到的就是对于左右指针每次逼近最大的，从而满足贪心的情况，从某个角度来看该题目也不算特别复杂。
class Solution:
def maxArea(self, height: List[int]) -> int:
left, right = 0, len(height) - 1
max_square = min(height[left], height[right]) * (right - left)
while left < right:
if height[left] < height[right]:
left += 1
else:
right -= 1
max_square = max(max_square, min(height[left], height[right]) * (right - left))
return max_square
15. 三数之和
- 思路：常规来说其实就是$O(n^3)$但是这样肯定超时，所以可能的手段就是先排序然后用双指针变成两数之和问题。取中间一个数开始，两个方向搜负数即可。但是理论上是这样，题目难的地方其实在于去重的步骤。首先，需要对mid去重，即去除和之前相同的情况，其次在最后还需要分别对左值和右值去重。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums = sorted(nums)
res = []
len_n = len(nums)
for mid in range(len_n-2):
# 第一步去重
if mid > 0 and nums[mid] == nums[mid-1]:
continue
l , r = mid + 1, len_n - 1
mid_v = nums[mid]
while l < r:
if nums[l] + nums[r] > - mid_v:
r -= 1
elif nums[l] + nums[r] < - mid_v:
l += 1
else:
res.append([nums[l], mid_v, nums[r]])
# 跳过重复的左值
while l < r and nums[l] == nums[l+1]:
l += 1
# 跳过重复的右值
while l < r and nums[r] == nums[r-1]:
r -= 1
r -= 1
l += 1
return res
42. 接雨水
- 思路：其实这道题算是相当印象深刻的题目了，甚至能够一行写出来了已经。这道题思路也很简单，类似其他dp的题目，先从头往后利用双指针过一遍，每一遍开始时，左指针为当前的状态，右指针不断向右，如果遇到大于左指针的情况，就计算一下积水数量（在这个过程中是已经算上去的），上述一遍得到的是从左往右递增的情况，同理获取一遍从右往左递增的情况即可。
class Solution:
def trap(self, height: List[int]) -> int:
ln = len(height)
water = []
c_max = height[0]
res = 0
for i in range(ln):
if height[i] > c_max:
c_max = height[i]
water.append(0)
elif height[i] == c_max:
water.append(0)
else:
water.append(c_max-height[i])
a_water = []
height = height[::-1]
c_max = height[0]
for i in range(ln):
if height[i] > c_max:
c_max = height[i]
a_water.append(0)
elif height[i] == c_max:
a_water.append(0)
else:
a_water.append(c_max-height[i])
for i, j in zip(water, a_water[::-1]):
res += min(i, j)
return res
# 还有一个极端版本
class Solution:
def trap(self, height: List[int]) -> int:
return 0 if len(set(height)) == 1 else sum([min(max(height[:i+1]), max(height[i:])) - height[i] for i in range(len(height))])
题解-滑动窗口
3. 无重复字符的最长子串
- 思路：说实话我感觉滑动窗口就是双指针的另一种形式罢了，如果没有重复的r+=1，否则l+=1直到没有重复。至于存储方式，用哈希表就好了。稍微借鉴一下前面set的使用方式了。
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if len(s) == 0:
return 0
l, r = 0, 0
hasht = set()
ls = len(s)
ml = 1
while r < ls:
if s[r] not in hasht:
hasht.add(s[r])
r += 1
else:
ml = max(ml , r - l)
hasht -= set(s[l])
l += 1
return max(ml, r-l)
438. 找到字符串中所有字母异位词
- 思路1:很简单我都不想多说：
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
sp = "".join(sorted(p))
lsp, ls = len(sp), len(s)
res = []
for i in range(ls - lsp + 1):
if "".join(sorted(s[i:i+lsp])) == sp:
res.append(i)
return res
- 思路2:这个就复杂一点了，字符中是否出现的次数，如果超了则l+=1。
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
ans = []
cnt = Counter(p) # 统计 p 的每种字母的出现次数
left = 0
for right, c in enumerate(s):
cnt[c] -= 1 # 右端点字母进入窗口
while cnt[c] < 0: # 字母 c 太多了
cnt[s[left]] += 1 # 左端点字母离开窗口
left += 1
if right - left + 1 == len(p): # s' 和 p 的每种字母的出现次数都相同
ans.append(left) # s' 左端点下标加入答案
return ans
题解-子串
560. 和为 K 的子数组
- 思路：注意题目，这道题不能排序做！从这个角度看的话其实就是更加复杂的两数之和问题了。由于是连续子串，所以最先想到的其实就是前缀和，在这种情况下，取差即可得到对应的结果：
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
ln = len(nums)
sum_n = [0] + [sum(nums[:i]) for i in range(1, ln+1)]
lsum_n = len(sum_n)
res = 0
for i in range(lsum_n-1):
for j in range(i+1, lsum_n):
if sum_n[j] - sum_n[i] == k:
res += 1
return res
尽管上述方法很简答，但是问题在于上述解答会超时。但是这种情况并不是因为前缀和的方法导致的，而是就差一步了，在这种情况下得考虑一下优化手段了。一下能想到的方案有两种：1、由于已经是前缀了，所以可以做一下排序之后只计算idx更大的即可。2、尝试保存一下其中的一些值。
这里尝试用第二种方案来解决，同时这种方案也是比较常用的手法。首先计算出前缀和数组s，之后会存在$s[j]-s[i] = k (i<j)$我们换一下顺序就好理解了，存在$s[j]-k = s[i]$，因此根据上式，计算$s[i]$的个数，等价于计算在 $s[j]$ 左边的 $s[j]−k$ 的个数。示例代码如下：
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
ln = len(nums)
sum_n = [0] * (len(nums) + 1)
for i, x in enumerate(nums):
sum_n[i + 1] = sum_n[i] + x
res_d = defaultdict(int)
ans = 0
for i in sum_n:
ans += res_d[i - k]
res_d[i] += 1
return ans
从代码的角度分析，首先sum_n还是刚才设计的内容。关键在于res_d的设计，但是还是太复杂了，我觉得可以从另一个角度再次简单理解一下。res_d保存的是之前的s[i]值，如果存在的话就使得ans+= res_d[i-k]。整体设计的非常巧妙！
for i in sum_n:
ans += res_d[i - k]
res_d[i] += 1
实际核心就是这两行，一个保证j在i后面，一个用来保存之前的值，分开都不行。
239. 滑动窗口最大值
- 思路：这种还是双指针+滑动窗口滑着就把结果搞出来了。但是由于最大值的获取是$O(N)$复杂度，所以很容易就超时了，首先是一个简单版本的滑动窗口：
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
if len(nums) <= 1 or k == 1:
return nums
r = k
res = []
cmax = max(nums[:r])
while r < len(nums):
res.append(cmax)
if nums[r] > cmax:
cmax = nums[r]
r += 1
if nums[r-k-1] == cmax:
cmax = max(nums[r-k:r])
res.append(cmax)
return res
这个倒是不难思考，但是问题在于，超时了！但是身为有着较强算法思维的我们而言，其实最好的方法就是在滑动窗口的值中维护一个优先队列，此外还有一种实现就是维护一个双端队列，这里把两种都写一下。当然，具体的数据结构就不用我们自己写了，
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
ans = []
q = deque() # 双端队列
for i, x in enumerate(nums):
# 1. 入
while q and nums[q[-1]] <= x:
q.pop() # 维护 q 的单调性
q.append(i) # 入队
# 2. 出
if i - q[0] >= k: # 队首已经离开窗口了
q.popleft()
# 3. 记录答案
if i >= k - 1:
# 由于队首到队尾单调递减，所以窗口最大值就是队首
ans.append(nums[q[0]])
return ans
## 双端队列
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
# 注意 Python 默认的优先队列是小根堆
q = [(-nums[i], i) for i in range(k)]
heapq.heapify(q)
ans = [-q[0][0]]
for i in range(k, n):
heapq.heappush(q, (-nums[i], i))
while q[0][1] <= i - k:
heapq.heappop(q)
ans.append(-q[0][0])
return ans
## 最大堆
当然，从具体实现上来看，我还是更倾向于使用双端队列。
76. 最小覆盖子串
- 思路：思路倒是不复杂，一个动长的滑动窗口，先把每个遇到的字符添加到字典里，如果遇到最近的就修改字典，整体思路这样，但是要是写出来还是有难度的，考虑到题目的难度，这里暂且先看一下Counter的一个用法：
class Counter():
...
def __le__(self, other):
'True if all counts in self are a subset of those in other.'
if not isinstance(other, Counter):
return NotImplemented
return all(self[e] <= other[e] for c in (self, other) for e in c)
我们可以看到，Counter实际上是自带大小比较的功能，而且实现也非常好理解。所以可以利用这个方便的和结果的子串进行比较：
cnt_s = Counter()
cnt_t = Counter(t)
...
if cnt_s < cnt_t:
...
所以整体的解决方案为：
class Solution:
def minWindow(self, s: str, t: str) -> str:
ans_left, ans_right = -1, len(s)
cnt_s = Counter() # s 子串字母的出现次数
cnt_t = Counter(t) # t 中字母的出现次数
left = 0
for right, c in enumerate(s): # 移动子串右端点
cnt_s[c] += 1 # 右端点字母移入子串
while cnt_s >= cnt_t: # 涵盖
if right - left < ans_right - ans_left: # 找到更短的子串
ans_left, ans_right = left, right # 记录此时的左右端点
cnt_s[s[left]] -= 1 # 左端点字母移出子串
left += 1
return "" if ans_left < 0 else s[ans_left: ans_right + 1]
题解-普通数组
53. 最大子数组和
- 思路：这题一眼就是dp，根本和普通数组没啥关系，但是既然这样搞了咱也得会做。首先，最简单粗暴的思路自然就是一整个$O(n^2)$的循环，但是包超时的。对于DP的思路，其实也很简单，跟当前最长的比即可。由于其是连续的最大，对于一个样例
[-2, 1, -3]显然如果前面的值小于0，则肯定不会连续上去。因此根据这个列一下条件转移方程试试，长度可以直接用一个变量保存，需要保存的状态应该是之前的连续和的最大值，无非就是自己和前一个的和的比较，所以代码如下：
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
c_max = -inf
ln = len(nums)
res = [-inf for i in range(ln+1)]
for i in range(1, ln+1):
res[i] = max(res[i-1]+nums[i-1], nums[i-1])
c_max = max(res[i], c_max)
# print(res)
return c_max
我真厉害嘿嘿。
56. 合并区间
- 思路：这个看数组长度，可以直接用$O(n^2)$解决，所以直接暴力拿下：
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort()
ci = intervals.pop(0)
res = []
while intervals:
new = intervals.pop(0)
if new[0] <= ci[1]:
if new[1] > ci[1]:
ci[1] = new[1]
else:
res.append(ci)
ci = new
res.append(ci)
return res
其实用了一个$O(n)$的pop操作，理论上也可以不用的，只是这里为了简化实现所以这样用了。这种题倒是有很多类似的题型。
189. 轮转数组
- 思路：如果不考虑原地置换的话应该秒杀了，但是现在高阶也建议了用$O(1)$所以不能直接拷贝空间解决。
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
nums[:] = nums[-k % n:] + nums[:-k % n]
这种解法算是python的语法糖，但是实际上应该使用了额外空间的。另一种很巧的思路如下：
轮转k个元素等于前n-k个反转之后后k个反转最后再一整个反转（这个有点类似以前做的矩阵旋转），直接开始写：
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
k = k % n
nums[:n-k] = nums[:n-k][::-1]
nums[n-k:] = nums[n-k:][::-1]
nums[:] = nums[::-1]
238. 除自身以外数组的乘积
- 思路：本来很简单的，但是不能做除法而且复杂度$O(n)$。那就直接不能一个一个暴力计算了。这道题算是比较巧妙地一种解法，核心在于
前缀，想到这一点的话会发现nums[i]部分的结果就是<i和>i的数值的相乘，所以开两个空间算一下试试：
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
pre = [1] * n
post = [1] * n
for i in range(1, n):
pre[i] = nums[i-1] * pre[i-1]
for i in range(n-2, -1, -1):
post[i] = post[i+1] * nums[i+1]
return [p*s for p,s in zip(pre, post)]
那能不能直接用$O(1)$来解，其实也可以，只要pre在向前的时候顺便计算一下就好了：
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
suf = [1] * n
for i in range(n - 2, -1, -1):
suf[i] = suf[i + 1] * nums[i + 1]
pre = 1
for i, x in enumerate(nums):
# 此时 pre 为 nums[0] 到 nums[i-1] 的乘积，直接乘到 suf[i] 中
suf[i] *= pre
pre *= x
return suf
41. 缺失的第一个正数
- 思路：如果用这个代码解决的话，已经相当接近最终的方法了但是实际上并不正确：
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
maxn = max(nums) + 1
space_min = inf
not1 = 1
for i in nums:
if i <= 0 :
continue
elif i == not1:
not1 += 1 # 已经很接近了
else :
if (i - 1) < space_min and (i - 1) != not1:
space_min = i - 1
else:
maxn = i + 1
return min(space_min, maxn, not1)
因为没有充分考虑有些分隔的问题，而这道题正确的求解方法是原地哈希，其核心就是把n个数字放到n-1个位置直到找到不对劲的，从理论上来说有点像排序，但是由于很多数字不满足情况，所以是会踢出去的。所以试一下看看效果：
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
for i in range(n):
while 1 <= nums[i] <= n and nums[nums[i] - 1] != nums[i]:
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
for i in range(n):
if nums[i] != i + 1:
return i + 1
return n + 1
题解-矩阵
73. 矩阵置零
- 思路：使用$O(mn)$和$O(m+n)$思路都不太行，毕竟最好还是$O(1)$空间而且既然可以就往这个方向想。原地的话一般都是使用原本的数据结构做数据存储，这道题也不例外，我们可以把其中的第一个出现0的行和列作为标记并处理即可，因此代码如下：
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
l_row, l_col = len(matrix), len(matrix[0])
sign_row, sign_col = None, None
for i in range(l_row):
for j in range(l_col):
if sign_row is None and matrix[i][j] == 0:
sign_row, sign_col = i, j
matrix[sign_row][sign_col] = None
if sign_row is None:
return
for i in range(l_row):
if i == sign_row:
continue
if 0 in matrix[i]:
matrix[i][sign_col] = None
for i in range(l_col):
if i == sign_col:
continue
for j in range(l_row):
if matrix[j][i] == 0:
matrix[sign_row][i] = None
break
print(matrix)
for i in range(l_row):
if matrix[i][sign_col] is None:
for j in range(l_col):
if matrix[i][j] is None:
continue
else:
matrix[i][j] = 0
for i in range(l_col):
if matrix[sign_row][i] is None:
for j in range(l_row):
if matrix[j][i] is None:
continue
else:
matrix[j][i] = 0
for i in range(l_row):
for j in range(l_col):
if matrix[i][j] is None:
matrix[i][j] = 0
54. 螺旋矩阵
- 思路：最近才做过，用四个指针表示深度即可：
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix:
return []
m, n = len(matrix), len(matrix[0])
res = []
def spiral_layer(sx, sy, rows, cols):
if rows <= 0 or cols <= 0:
return
# 上：从左到右
for i in range(sx, sx + cols):
res.append(matrix[sy][i])
# 右：从上到下（至少两行）
if rows > 1:
for j in range(sy + 1, sy + rows):
res.append(matrix[j][sx + cols - 1])
# 下：从右到左（至少两列）
if cols > 1:
for i in range(sx + cols - 2, sx - 1, -1):
res.append(matrix[sy + rows - 1][i])
# 左：从下到上（至少三行）
if rows > 2:
for j in range(sy + rows - 2, sy, -1):
res.append(matrix[j][sx])
# 递归处理内层
spiral_layer(sx + 1, sy + 1, rows - 2, cols - 2)
spiral_layer(0, 0, m, n)
return res
48. 旋转图像
- 思路：这个也算是比较巧的思路，既然是原地旋转的话肯定还是找个规律做置换了，所以直接先对角线翻转再上下翻转即可
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
mr = int(n//2)
for r in range(mr):
for c in range(n):
matrix[r][c], matrix[n-r-1][c] = matrix[n-r-1][c], matrix[r][c]
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
return matrix
240. 搜索二维矩阵 II
- 思路：不幸的是题目的长度很小所以直接两轮for循环也能解决。
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
l_row, l_cow = len(matrix), len(matrix[0])
for i in range(l_row):
for j in range(l_cow):
if matrix[i][j] == target:
return True
return False
当然，为了追求效率，我们还是尽可能用高效的算法来解决。按常理来说其实更倾向于通过二分来查找（毕竟已经排好序），但是常规的二分对应的是一维数组，这种情况下其实我们考虑对角线？首先，对于斜对角，每个值都是大于前面矩阵的值，所以可以两次二分解决一下，先左上到右下，之后在从左下到右上。
- 其他的思路很多，这里简答拿一张图说明一下：
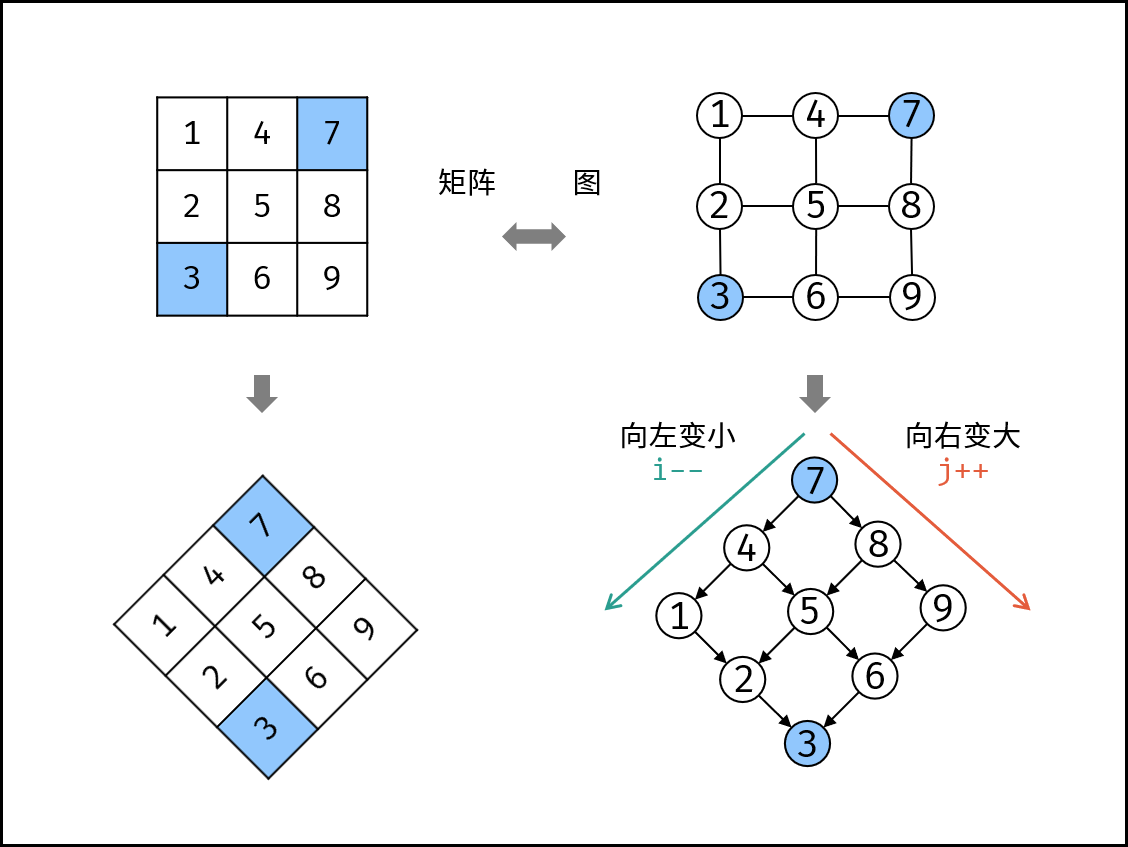
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
i, j = len(matrix) - 1, 0
while i >= 0 and j < len(matrix[0]):
if matrix[i][j] > target: i -= 1
elif matrix[i][j] < target: j += 1
else: return True
return False
题解-链表
160. 相交链表
- 思路：题目设计的比较畸形，其实就是找相同值，一般来说合适的解法就是先遍历存储然后找节点，但是题目建议$O(m+n)$时间复杂度和$O(1)$空间复杂度。考虑到链表的数据结构，如果有公共部分，则假设公共长度为$a$则两个链表剩下的长度$m-a$和$n-a$，为了对齐，先让长一点的链表走$m-n$个元素，之后直到遇到相同元素就好了。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
len_a, len_b = 0, 0
cur_node = headA
while cur_node:
len_a += 1
cur_node = cur_node.next
cur_node = headB
while cur_node:
len_b += 1
cur_node = cur_node.next
longer = headA if len_a > len_b else headB
shorter = headB if len_a > len_b else headA
for i in range(abs(len_a-len_b)):
longer = longer.next
while longer or shorter:
if id(longer) == id(shorter):
return longer
longer = longer.next
shorter = shorter.next
return None
这道题的一个核心细节是判断相交的情况：if id(longer) == id(shorter)不能仅仅判断值相等。
206. 反转链表
- 思路：看似简单实则一点都不简单。建议是画个图表示一下：
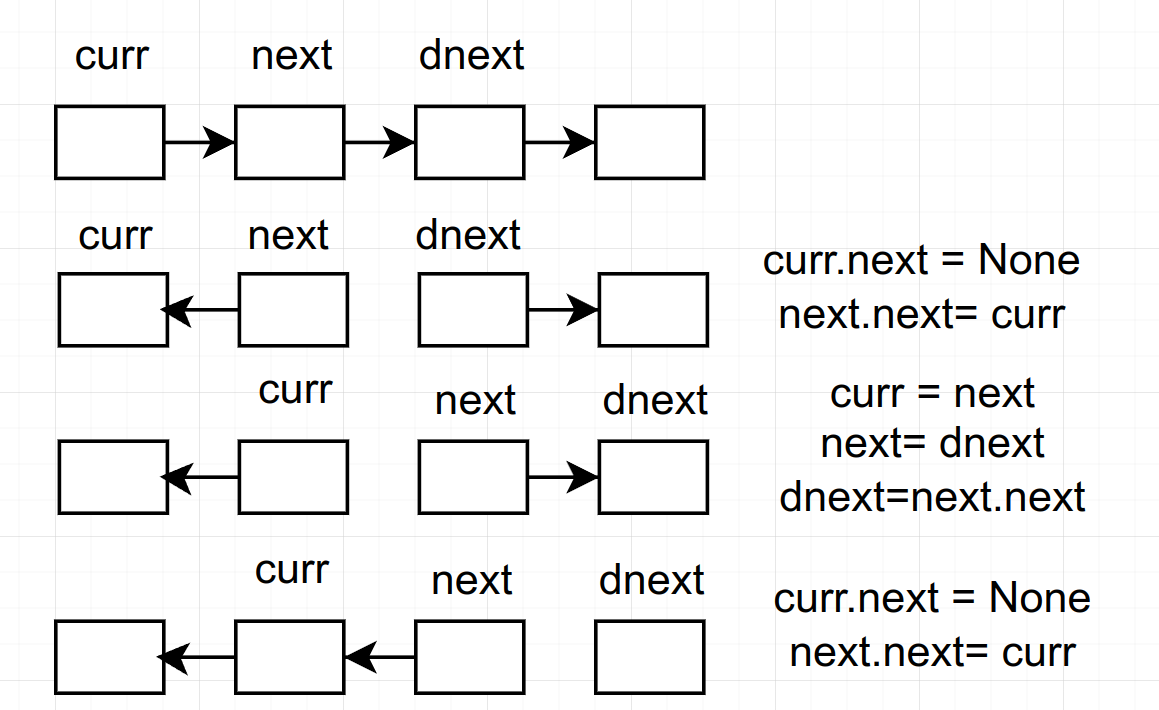
所以只需要使用三个链表就好了，但是要稍微处理下两个问题：1、开始时的None 2、边界条件。
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
curr = head
prev = None
while curr != None:
next = curr.next
curr.next = prev
prev = curr
curr = next
return prev
234. 回文链表
- 思路：很多思路，但是最好还是按$O(1)$空间复杂度解决。首先链表长度$len$是肯定需要获取的。之后把前$len//2$个元素给反转之后继续双向遍历就好了。
class Solution:
# 876. 链表的中间结点
def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
# 206. 反转链表
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
pre, cur = None, head
while cur:
nxt = cur.next
cur.next = pre
pre = cur
cur = nxt
return pre
def isPalindrome(self, head: Optional[ListNode]) -> bool:
mid = self.middleNode(head)
head2 = self.reverseList(mid)
while head2:
if head.val != head2.val: # 不是回文链表
return False
head = head.next
head2 = head2.next
return True
141. 环形链表
- 思路：快慢指针秒了
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
slow = fast = head # 乌龟和兔子同时从起点出发
while fast and fast.next:
slow = slow.next # 乌龟走一步
fast = fast.next.next # 兔子走两步
if fast is slow: # 兔子追上乌龟（套圈），说明有环
return True
return False # 访问到了链表末尾，无环
142. 环形链表 II
- 思路：还是快慢指针，但是这次要返回环的位置所以需要一些数学运算了。假设不带环的长度为$L$，假设环前面长度为$a$，后面为$b$:
image-20250219155741783
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if fast is slow:
while slow is not head:
slow = slow.next
head = head.next
return slow
return None
21. 合并两个有序链表
- 思路：主要是编写上的难度
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
cur = dummy = ListNode() # 用哨兵节点简化代码逻辑
while list1 and list2:
if list1.val < list2.val:
cur.next = list1 # 把 list1 加到新链表中
list1 = list1.next
else: # 注：相等的情况加哪个节点都是可以的
cur.next = list2 # 把 list2 加到新链表中
list2 = list2.next
cur = cur.next
cur.next = list1 or list2 # 拼接剩余链表
return dummy.next
这里用了个非常细节的设计cur.next = list1 or list2，简而言之就是把不为None的添加到尾部，算是一个很新颖的用法了。
2. 两数相加
- 思路：这道题的设计就决定了肯定不会限制空间复杂度，所以随便秒杀
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
l1v, l2v = "", ""
while l1:
l1v += str(l1.val)
l1 = l1.next
while l2:
l2v += str(l2.val)
l2 = l2.next
dummy = ListNode(None)
curr = dummy
for i in str(eval(l1v[::-1] + "+" + l2v[::-1]))[::-1]:
newn = ListNode(int(i))
curr.next = newn
curr = curr.next
curr.next = None
return dummy.next
19. 删除链表的倒数第 N 个结点
思路：由于不限制复杂度，所以遍历两遍就行了，但是最好可以有更好的思路，比如先后指针。先让一个指针走N个即可：
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
# 由于可能会删除链表头部，用哨兵节点简化代码
left = right = dummy = ListNode(next=head)
for _ in range(n):
right = right.next # 右指针先向右走 n 步
while right.next:
left = left.next
right = right.next # 左右指针一起走
left.next = left.next.next # 左指针的下一个节点就是倒数第 n 个节点
return dummy.next
### 另一种好写的：
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy = ListNode(next=head)
ll = 0
while head:
ll += 1
head = head.next
head = dummy
for i in range(ll-n):
head = head.next
head.next = head.next.next
return dummy.next
24. 两两交换链表中的节点
- 思路：其实并不复杂。还是得想办法画个图，此外为了避免一些奇怪的情况，可以考虑创建哨兵节点：
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
node0 = dummy = ListNode(next=head) # 用哨兵节点简化代码逻辑
node1 = head
while node1 and node1.next: # 至少有两个节点
node2 = node1.next
node3 = node2.next
node0.next = node2 # 0 -> 2
node2.next = node1 # 2 -> 1
node1.next = node3 # 1 -> 3
node0 = node1 # 下一轮交换，0 是 1
node1 = node3 # 下一轮交换，1 是 3
return dummy.next # 返回新链表的头节点
25. K 个一组翻转链表
- 思路：反转链表升级版，先获取长度然后对于每k个反转一下即可，可以直接拿之前的code试试：
class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
n = 0
cur = head
while cur:
n += 1
cur = cur.next
p0 = dummy = ListNode(next=head)
pre = None
cur = head
while n >= k:
n -= k
for _ in range(k):
nxt = cur.next
cur.next = pre
pre = cur
cur = nxt
nxt = p0.next
nxt.next = cur
p0.next = pre
p0 = nxt
return dummy.next
题解-树
94. 二叉树的中序遍历
- 思路：很简单了，实例代码：
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
而且这个算是比较通用的实现，对于不同的遍历方式改一下返回值的相加顺序就好了
104. 二叉树的最大深度
- 思路：dfs一下即可，或者层序遍历
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root: return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
226. 翻转二叉树
- 思路：翻转一下兄弟节点（包括None节点）：
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
101. 对称二叉树
- 思路：起初感觉有点绕，实际上设置一个isSameTree函数之后每次左右子树对应进去一下就好了
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
def isSameTree(ln, rn):
if ln is None or rn is None:
return ln is rn
return ln.val == rn.val and isSameTree(ln.left, rn.right) and isSameTree(ln.right, rn.left)
return isSameTree(root.left, root.right)
543. 二叉树的直径
- 思路：找最长路径其实通常是图论该干的，但是可惜这道题是树，最简单的思路就是拿maxdepth每个节点测一下求最大值，如下：
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root: return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
if not root: return 0
res = self.maxDepth(root.left) + self.maxDepth(root.right)
return max(res, self.diameterOfBinaryTree(root.left), self.diameterOfBinaryTree(root.right))
不幸的是超时了，所以合理的手段其实还是dfs，但是两个子节点之间的路径得减去祖父节点的深度即可。
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
self.ans = 1
def dfs(node):
if not node:
return 0
L = dfs(node.left)
R = dfs(node.right)
self.ans = max(self.ans, L + R + 1)
return max(L, R) + 1
dfs(root)
return self.ans - 1
可恶，其实和求深度差不多，只是稍微多了一行。
102. 二叉树的层序遍历
- 思路：我是数据结构高手所以我知道这道题用队列：
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root: return []
l = [[root, 0]]
res = defaultdict(list)
while l:
cur = l.pop(0)
if cur[0].left is not None:
l.append([cur[0].left, cur[1]+1])
if cur[0].right is not None:
l.append([cur[0].right, cur[1]+1])
res[cur[1]].append(cur[0].val)
return [res[i] for i in res]
秒了，但是看看题解：
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
q = deque([root])
while q:
vals = []
for _ in range(len(q)):
node = q.popleft()
vals.append(node.val)
if node.left: q.append(node.left)
if node.right: q.append(node.right)
ans.append(vals)
return ans
从长远的角度来看，其实用真实的队列会更好一点。
108. 将有序数组转换为二叉搜索树
- 思路：逐渐娴熟了，只要每次把中间的数值作为节点并把左右侧数组传入即可。
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums: return TreeNode(None)
midN = len(nums) // 2
root = TreeNode(nums[midN])
root.left = self.sortedArrayToBST(nums[:midN])
root.right = self.sortedArrayToBST(nums[midN+1:])
return root
98. 验证二叉搜索树
- 思路：很简单，但是这里强推一下这种写法：
class Solution:
def isValidBST(self, root: Optional[TreeNode], left=-inf, right=inf) -> bool:
if root is None:
return True
x = root.val
return left < x < right and \
self.isValidBST(root.left, left, x) and \
self.isValidBST(root.right, x, right)
避免了蛋疼的判断
230. 二叉搜索树中第 K 小的元素
- 思路：中序遍历一下即可（至今不知道黄大人当时的变量为什么找不到）
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
res = []
def innerorder(root):
if not root: return
innerorder(root.left)
res.append(root.val)
innerorder(root.right)
innerorder(root)
return res[k-1]
199. 二叉树的右视图
- 思路：层序遍历输出-1索引的即可（修改一行就好了）
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root: return []
l = [[root, 0]]
res = defaultdict(list)
while l:
cur = l.pop(0)
if cur[0].left is not None:
l.append([cur[0].left, cur[1]+1])
if cur[0].right is not None:
l.append([cur[0].right, cur[1]+1])
res[cur[1]].append(cur[0].val)
return [res[i][-1] for i in res]
114. 二叉树展开为链表
- 思路：如果不看原地更换的话就很简单了。
class Solution:
def flatten(self, root: TreeNode) -> None:
preorderList = list()
def preorderTraversal(root: TreeNode):
if root:
preorderList.append(root)
preorderTraversal(root.left)
preorderTraversal(root.right)
preorderTraversal(root)
size = len(preorderList)
for i in range(1, size):
prev, curr = preorderList[i - 1], preorderList[i]
prev.left = None
prev.right = curr
105. 从前序与中序遍历序列构造二叉树
- 思路：根据先序和中序遍历构造二叉树，每次从前序找到第一个元素，然后从中序中索引一下这个元素，则左子树由中序索引左侧组成，右子树相反。所以主要是编码的难度：
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder: # 空节点
return None
left_size = inorder.index(preorder[0]) # 左子树的大小
left = self.buildTree(preorder[1: 1 + left_size], inorder[:left_size])
right = self.buildTree(preorder[1 + left_size:], inorder[1 + left_size:])
return TreeNode(preorder[0], left, right)
上述的算法实际上就已经可以解决了，但是有个细节问题，由于涉及到了index操作，所以会有及$O(N)$时间复杂度，整体的复杂度也会到达$O(N^2)$，所以可以考虑使用字典存储一下索引来优化，这里就不多说明了
437. 路径总和 III
- 思路：可以想到是前缀和的思路，但是相较于数组结构，每个节点得知道之前的所有节点的值，所以这道题的难度变成了一个数据结构的问题：
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
def dfs(root, count, sumption):
if root is None:
return 0
sumption += root.val
res = count[sumption-targetSum]
count[sumption] += 1
res += dfs(root.left, count, sumption)
res += dfs(root.right, count, sumption)
count[sumption] -= 1 # 会干扰左右子树的计算
return res
return dfs(root, Counter({0:1}), 0)
核心其实在于这个 count[sumption] -= 1，如何不移除之前的节点，会导致在计算左子树的时候使用右子树的值继续计算，当然，基于上述情况也可以把临时的Counter删除了，所以总体答案如下：
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
c = Counter([0])
def dfs(root, sumption):
if root is None:
return 0
sumption += root.val
res = c[sumption-targetSum]
c[sumption] += 1
res += dfs(root.left, sumption)
res += dfs(root.right, sumption)
c[sumption] -= 1 # 会干扰左右子树的计算
return res
return dfs(root, 0)
236. 二叉树的最近公共祖先
- 思路：回溯时的解决问题，首先假设是两棵子树，则每个子树按返回值判断即可，同时也要判断一下在同一枝干上的情况：
class Solution:
def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
if root in (None, p, q):
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left and right: # 左右都找到
return root # 当前节点是最近公共祖先
return left or right
给灵神跪了，简单但是不简约。这种思维确实厉害。
200. 岛屿数量
- 思路：做dfs的时候插旗子，遇到的第一个设置为1即可
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
def dfs(i: int, j: int) -> None:
# 出界，或者不是 '1'，就不再往下递归
if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] != '1':
return
grid[i][j] = '2' # 插旗！避免来回横跳无限递归
dfs(i, j - 1) # 往左走
dfs(i, j + 1) # 往右走
dfs(i - 1, j) # 往上走
dfs(i + 1, j) # 往下走
ans = 0
for i, row in enumerate(grid):
for j, c in enumerate(row):
if c == '1': # 找到了一个新的岛
dfs(i, j) # 把这个岛插满旗子，这样后面遍历到的 '1' 一定是新的岛
ans += 1
return ans
994. 腐烂的橘子
- 思路：算是前面题目的升级版，但是用两个列表分别保存当前和下一个阶段的即可，但是要考虑的情况可能稍微多了一点
class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
lrow, lcol = len(grid), len(grid[0])
s_list, c_list = [], []
for i in range(lrow):
for j in range(lcol):
if grid[i][j] == 2:
s_list.append([i,j])
def rotOrange(i, j):
resl = []
if i + 1 < lrow and grid[i+1][j] == 1:
resl.append([i+1, j])
grid[i+1][j] = -1
if i - 1 >=0 and grid[i-1][j] == 1:
resl.append([i-1, j])
grid[i-1][j] = -1
if j + 1 < lcol and grid[i][j+1] == 1:
resl.append([i, j+1])
grid[i][j+1] = -1
if j - 1 >= 0 and grid[i][j-1] == 1:
resl.append([i, j-1])
grid[i][j-1] = -1
return resl
times = 0
while s_list:
print(s_list)
c_list, s_list = s_list, []
for i in c_list:
grid[i[0]][i[1]] = -1
s_list += rotOrange(i[0], i[1])
if s_list == []:
break
else:
times += 1
for i in range(lrow):
for j in range(lcol):
if grid[i][j] == 1:
return -1
return times
虽然想着很简单但是要完全写对还是相当有难度的，整体的难点在于如何保证s_list去重而且让s_list不存在c_list内容，否则会重复计算。在我的实现里面由于是每次进行BFS，所以在去重时会带来很大的麻烦，最好的方法还是参考一下灵神的：
class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
fresh = 0
q = []
for i, row in enumerate(grid):
for j, x in enumerate(row):
if x == 1:
fresh += 1 # 统计新鲜橘子个数
elif x == 2:
q.append((i, j)) # 一开始就腐烂的橘子
ans = 0
while q and fresh:
ans += 1 # 经过一分钟
tmp = q
q = []
for x, y in tmp: # 已经腐烂的橘子
for i, j in (x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1): # 四方向
if 0 <= i < m and 0 <= j < n and grid[i][j] == 1: # 新鲜橘子
fresh -= 1
grid[i][j] = 2 # 变成腐烂橘子
q.append((i, j))
return -1 if fresh else ans
可恶，真厉害
207. 课程表
- 思路：拓扑排序，本来以为很复杂，实际上就是找入度为0的，直到所有课程结束。
from typing import List
from collections import deque
class Solution:
# 思想：该方法的每一步总是输出当前无前趋（即入度为零）的顶点
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
"""
:type numCourses: int 课程门数
:type prerequisites: List[List[int]] 课程与课程之间的关系
:rtype: bool
"""
# 课程的长度
clen = len(prerequisites)
if clen == 0:
# 没有课程，当然可以完成课程的学习
return True
# 步骤1：统计每个顶点的入度
# 入度数组，记录了指向它的结点的个数，一开始全部为 0
in_degrees = [0 for _ in range(numCourses)]
# 邻接表，使用散列表是为了去重
adj = [set() for _ in range(numCourses)]
# 想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]
# [0, 1] 表示 1 在先，0 在后
# 注意：邻接表存放的是后继 successor 结点的集合
for second, first in prerequisites:
in_degrees[second] += 1
adj[first].add(second)
# 步骤2：拓扑排序开始之前，先把所有入度为 0 的结点加入到一个队列中
# 首先遍历一遍，把所有入度为 0 的结点都加入队列
queue = deque()
for i in range(numCourses):
if in_degrees[i] == 0:
queue.append(i)
counter = 0
while queue:
top = queue.popleft()
counter += 1
# 步骤3：把这个结点的所有后继结点的入度减去 1，如果发现入度为 0 ，就马上添加到队列中
for successor in adj[top]:
in_degrees[successor] -= 1
if in_degrees[successor] == 0:
queue.append(successor)
return counter == numCourses
灵神还给出了另一种思路：判断是否有环
题解-回溯
46. 全排列
- 思路：最简单的想法其实就是构建这个树之后做dfs即可，但是在简化理解之后实际上连树也不需要构建，这里要用到之前做到的一道题的思想
这道题目核心在于完成一个路径节点的计算之后会恢复回去，因此同样的，我们不需要构建完整的树，只需要做dfs，并保存每一层的状态即可。所以整体的思路如下：
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(permutations(nums))
还是写一下正解：
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ln = len(nums)
ans = []
path = [0] * ln
exist = [False] * ln
def dfs(depth):
if depth == ln:
ans.append(path.copy())
return
for j, on in enumerate(exist):
if not on:
path[depth] = nums[j]
exist[j] = True
dfs(depth + 1)
exist[j] = False
dfs(0)
return ans
78. 子集
- 思路：聪明的小伙伴应该能想到，直接使用上一道题目的代码即可，但是在添加的部分改一下：
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ln = len(nums)
ans = []
path = []
def dfs(depth):
if depth == ln:
ans.append(path.copy())
return
dfs(depth + 1)
path.append(nums[depth])
dfs(depth + 1)
path.pop()
dfs(0)
return ans
即便如此相较于上一道题目还是有相当多的差别的，但是核心思路还是dfs+恢复
- 思路：这个反而很简单，首先把所有的字符表示出来，之后构建树即可（和之前的思路几乎一致，只不过每次的数字编程数组罢了）。感觉理解了前面两道题目，这倒题目就好理解多了。
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if digits is "":
return []
rd = {"2":"abc", "3": "def", "4": "ghi", "5":"jkl", "6": "mno", "7": "pqrs", "8":"tuv", "9": "wxyz"}
all_rd = [rd[i] for i in digits]
ln = len(all_rd)
path = []
res = []
def dfs(depth):
if depth == ln:
res.append("".join(path))
return
for c in all_rd[depth]:
path.append(c)
dfs(depth + 1)
path.pop()
dfs(0)
return res
39. 组合总和
- 思路：还是一样的思路，到目前为止其实都不需要专门做去重的步骤，但是这道题就需要了：
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
ans = []
def dfs(sn):
if sn == target:
ans.append(path.copy())
elif sn > target:
return
for c in candidates:
path.append(c)
dfs(sn + c)
path.pop()
dfs(0)
return ans
# 输出：[[2,2,2,2],[2,3,3],[3,2,3],[3,3,2],[3,5],[5,3]]
# 预期结果：[[2,2,2,2],[2,3,3],[3,5]]
上述思路倒是和题目完全一致，但是问题在于上述思路无法去重，合理的思路是对list做排序之后用set做去重，由于题目说了长度不超过150所以显然是可行的。但是要是想更加优雅地解决的话就得引入去重了（剪枝），当然，灵神的题解也给的非常优秀。举一个简单的例子，如果我们每次按当前的最小值放入，则会存在：[2,2,2,2], [2,2,4], [2,4,2]这样的情况，但是其实只要每次限制使用递增的情况，就能解决这种情况（woc我不会表述了）
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
path = []
ans = []
def dfs(i, left):
if left == 0:
ans.append(path.copy())
return
if i == len(candidates) or left < candidates[i]:
return
dfs(i + 1, left)
path.append(candidates[i])
dfs(i, left - candidates[i])
path.pop()
dfs(0, target)
return ans
这时候代码长这个样子，即优先选择值最大的情况。另一种写法如下：
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
ans = []
path = []
def dfs(i: int, left: int) -> None:
if left == 0:
# 找到一个合法组合
ans.append(path.copy())
return
if left < candidates[i]:
return
# 枚举选哪个
for j in range(i, len(candidates)):
path.append(candidates[j])
dfs(j, left - candidates[j])
path.pop() # 恢复现场
dfs(0, target)
return ans
相较于上一种，感觉还是这版代码更好理解，这种情况下出现的数组必然是递增的，因此不会出现重复的情况
22. 括号生成
- 思路：由于最终生成的结果必然是正确的，只需要保证栈不为空即可，如果仅仅只是判断数量的话就是$n!$，可惜这道题要返回所有可能的结果，就得稍微动点脑子了。从另一个角度分析的话，这道题其实就是在现有的情况下插入括号即可。因此另一个可能的解法就是首先得出所有括号的插入方法，之后在结果中生成即可。
- 其实做到目前为止，对于回溯的一个显然的思路就在于如何处理选或不选，全排序是每次都得选，子集是不选选过的，组合总和是选最大的，括号生成就是选择左括号或者小于左括号数量的右括号，所以代码如下：
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
ln = n * 2
path = [""] * ln
def dfs(i: int, open: int) -> None:
if i == ln: # 括号构造完毕
res.append(''.join(path)) # 加入答案
return
if open < n: # 可以填左括号
path[i] = '(' # 直接覆盖
dfs(i + 1, open + 1) # 多了一个左括号
if i - open < open: # 可以填右括号
path[i] = ')' # 直接覆盖
dfs(i + 1, open)
dfs(0, 0)
return res
原本是打算用range做的，结果就是多了很多没用的结果，实际上只要每次dfs的时候判断就好了，反正回溯的时候会实现循环。
79. 单词搜索
- 思路：不想什么优化思路，做dfs即可：
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m, n = len(board), len(board[0])
def dfs(i: int, j: int, k: int) -> bool:
if board[i][j] != word[k]: # 匹配失败
return False
if k == len(word) - 1: # 匹配成功！
return True
board[i][j] = '' # 标记访问过
for x, y in (i, j - 1), (i, j + 1), (i - 1, j), (i + 1, j): # 相邻格子
if 0 <= x < m and 0 <= y < n and dfs(x, y, k + 1):
return True # 搜到了！
board[i][j] = word[k] # 恢复现场
return False # 没搜到
return any(dfs(i, j, 0) for i in range(m) for j in range(n))
呜呜呜学不会这么优化的代码，虽然思路一样但是完全不一样。虽然是回溯但是这道题的回溯思路只在恢复现场那一行出现了，有点可惜。
131. 分割回文串
- 思路：简单点想的话，其实就是找到最长的回文串，之后不断做切分即可（因此得从右往左进行）。但是这种思路有点违背这部分的内容，因此这类题目的另一类思路是，是否要插入逗号。或者说从现在开始的res-n个字符是否是回文串，因此代码如下：
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
ls = len(s)
path = []
def dfs(depth):
if depth == ls:
res.append(path.copy())
return
for i in range(depth, ls):
t = s[depth: i + 1]
if t == t[::-1]:
path.append(t)
dfs(i+1)
path.pop()
dfs(0)
return res
51. N 皇后
- 思路：现在再看n皇后问题其实完全不复杂了（完全想错了），最开始可能认为就是全排列+去掉对角线相同情况，但是实际上完全没那么简单，当然，全排列的代码可以拿过来，但是问题在于如何判断对角线已经存在对应的皇后：
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
conn = [("."*i + "Q" + "."*(n-i-1)) for i in range(n)]
nums = [i for i in range(n)]
ln = len(nums)
ans = []
path = [0] * ln
exist = [False] * ln
def dfs(depth):
if depth == ln:
ans.append([("."*i + "Q" + "."*(n-i-1)) for i in path])
return
for j, on in enumerate(exist):
if not on:
status = True
for idx, check in enumerate(path[:depth]):
if abs(depth - idx) == abs(nums[j] - path[idx]):
status = False
if status == False:
continue
path[depth] = nums[j]
exist[j] = True
dfs(depth + 1)
exist[j] = False
dfs(0)
return ans
本来想看题解，不幸的是一下子做出来了，核心就在于：(看来当天状态很好啊)
status = True
for idx, check in enumerate(path[:depth]):
if abs(depth - idx) == abs(nums[j] - path[idx]):
status = False
if status == False:
continue
题解-二分搜索
35. 搜索插入位置
- 思路：算是最基础的二分搜索了，详细参考这部分的模板代码
74. 搜索二维矩阵
- 思路：跟上一道题目一样，展开就好了：
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
lrow, lcol = len(matrix), len(matrix[0])
left, right = 0, (lrow * lcol) - 1
while left <= right:
mid = ( left + right ) // 2
mrow = mid // lcol
mcol = mid % lcol
if matrix[mrow][mcol] == target:
return True
elif matrix[mrow][mcol] > target:
right = mid - 1
else:
left = mid + 1
return False
34. 在排序数组中查找元素的第一个和最后一个位置
- 思路：毕竟说了二分，思路是稍微有点差距，可以先找到一个分界点，之后根据这个分界点，从左往右搜索和从右往左搜索。且看我丑陋的代码：
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
def searchInsert(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return -1
def searchl(nums, target):
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
right = mid - 1
else:
left = mid + 1
return left
def searchr(nums, target):
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
left = mid + 1
else:
right = mid - 1
return left
f = searchInsert(nums, target)
if f == -1:
return [-1, -1]
l = searchl(nums[:f], target)
r = searchr(nums[f:], target)
return [l, r+f-1]
可以使用库函数直接实现倒是：
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
start = bisect_left(nums, target)
if start == len(nums) or nums[start] != target:
return [-1, -1]
end = bisect_right(nums, target) - 1
return [start, end]
33. 搜索旋转排序数组
- 思路：首先想法是查中间的分割元素然后做二分，但是问题在于如果遍历查找的话是一个$O(N)$的复杂度，就不适合了。核心在于如何使用二分来迅速查找到中间的元素。其实和上一道题思路几乎一样，二分查找找到最小的小于nums[n-1]的元素即可。
class Solution:
def search(self, nums: List[int], target: int) -> int:
def searchmid(nums):
left, right = 0, len(nums) - 1
while left <= right:
mid = ( left + right ) // 2
if nums[mid] <= nums[-1]:
right = mid - 1
elif nums[mid] > nums[-1]:
left = mid + 1
return left
m = searchmid(nums)
def searchInsert(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return -1
print(m)
res = [searchInsert(nums[m:], target), searchInsert(nums[:m], target)]
if res[0] != -1:
return res[0] + m
return res[1]
153. 寻找旋转排序数组中的最小值
- 思路：上一道题目的简单版本
class Solution:
def findMin(self, nums: List[int]) -> int:
def searchmid(nums):
left, right = 0, len(nums) - 1
while left <= right:
mid = ( left + right ) // 2
if nums[mid] <= nums[-1]:
right = mid - 1
elif nums[mid] > nums[-1]:
left = mid + 1
return left
m = searchmid(nums)
return nums[m]
4. 寻找两个正序数组的中位数
- 思路：要求了$O(log(M+N))$复杂度所以变为困难题目了。太难了暂且搁置
题解-栈
20. 有效的括号
- 思路：用一个栈维护，如果到最后栈空就正确。
class Solution:
def isValid(self, s: str) -> bool:
stack = []
for i in s:
if i in "([{":
stack.append(i)
else:
if len(stack) == 0:
return False
c = stack.pop()
if c == "{" and i == "}" or c == "[" and i == "]" or c == "(" and i ==")":
continue
else:
return False
if len(stack) != 0:
return False
return True
155. 最小栈
- 思路：数据结构题目实现一个最小栈。用一个栈+一个最小栈就好了
class MinStack:
def __init__(self):
self.list = []
self.minl = [inf]
def push(self, val: int) -> None:
self.list.append(val)
if val <= self.minl[-1]:
self.minl.append(val)
def pop(self) -> None:
val = self.list.pop()
if val == self.minl[-1]:
self.minl.pop()
def top(self) -> int:
return self.list[-1]
def getMin(self) -> int:
return self.minl[-1]
题解-贪心算法
121. 买卖股票的最佳时机
- 思路：顷刻炼化
class Solution:
def maxProfit(self, prices: List[int]) -> int:
mp = 0
cur_i = inf
for i in prices:
cur_i = min(i, cur_i)
mp = max(mp, i - cur_i)
return mp
55. 跳跃游戏
- 思路：其他的不用考虑，只需要记录所能跳到的最远距离即可，同时记录当前的位置，如果超出了最远距离则说明无法达到，否则不断记录直到完成遍历
class Solution:
def canJump(self, nums: List[int]) -> bool:
md = 0
for i, jump in enumerate(nums):
if i > md:
return False
md = max(md, i + jump)
return True
45. 跳跃游戏 II
- 思路：两种思路，其一可以每次从当前出发，然后记录到达可以到达所有格子的最小跳数，此时代码如下：
class Solution:
def jump(self, nums: List[int]) -> int:
dp = [inf for _ in nums]
dp[0] = 0
for idx, i in enumerate(nums):
for j in range(1, i+1):
if idx + j < len(nums):
dp[idx + j] = min(dp[idx + j], dp[idx] + 1)
# print(dp)
return dp[-1]
虽然来说可以秒杀但是复杂度毕竟是达到了$O(N^2)$。另一种相对来说比较复杂一点了，判断当前跳的最远和能跳的距离中最远的：
class Solution:
def jump(self, nums: List[int]) -> int:
ans = 0
cur_right = 0 # 已建造的桥的右端点
next_right = 0 # 下一座桥的右端点的最大值
for i in range(len(nums) - 1):
# 遍历的过程中，记录下一座桥的最远点
next_right = max(next_right, i + nums[i])
if i == cur_right: # 无路可走，必须建桥
cur_right = next_right # 建桥后，最远可以到达 next_right
ans += 1
return ans
763. 划分字母区间
- 也不算复杂，记录一下当前字母的最远距离即可，然后当遇到最远距离就记录当前位置，所以整体思路还是不复杂的。
class Solution:
def partitionLabels(self, s: str) -> List[int]:
last = {c: i for i, c in enumerate(s)} # 每个字母最后出现的下标
ans = []
start = end = 0
for i, c in enumerate(s):
end = max(end, last[c]) # 更新当前区间右端点的最大值
if end == i: # 当前区间合并完毕
ans.append(end - start + 1) # 区间长度加入答案
start = i + 1 # 下一个区间的左端点
return ans
题解-动态规划
70. 爬楼梯
- 思路：现在知道为什么和斐波那契数列一养了，当然思路也很简单：
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
s1, s2 = 1, 2
for i in range(n-2):
s1, s2 = s2, s2+s1
return s2
题解-技巧
- 思路：对所有数字做异或，最后留下来的就是这个数字
class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for i in nums:
res ^= i
return res
169. 多数元素
- 思路：其实记录一下某个数据的频次，相同+1，不同-1，最后留下来的就是了：
class Solution:
def majorityElement(self, nums: List[int]) -> int:
curv = nums[0]
curtimes = 1
for i in nums[1:]:
if curv == i:
curtimes += 1
else:
curtimes -= 1
if curtimes < 0:
curtimes = 1
curv = i
return curv
75. 颜色分类
- 思路：就三个数字，直接遍历计算数量就好了
class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
d = Counter(nums)
for i in range(len(nums)):
if i < d[0]:
nums[i] = 0
elif i < d[0] + d[1]:
nums[i] = 1
else:
nums[i] = 2